Trang chủ / Xây dựng / *** / TCXD229:1999
Tiêu chuẩn xây dựng TCXD 229:1999 về Chỉ dẫn tính toán thành phần động của tải trọng gió theo TCVN 2737:1995
TIÊU CHUẨN XÂY DỰNG
TCXD 229 : 1999
CHỈ DẪN TÍNH TOÁN THÀNH PHẦN ĐỘNG CỦA TẢI TRỌNG GIÓ THEO TIÊU CHUẨN TCVN 2737 : 1995.
Guidance for determination of dynamic component of the wind loads under TCVN 2737 : 1995
1. Phạm vi áp dụng
1.1. Chỉ dẫn này dùng để tính toán thành phần động của tải trọng gió tác dụng lên các kết cấu, nền móng, nhà và công trình theo tiêu chuẩn tải trọng và tác động TCVN 2737 : 1995 [1].
1.2. Thành phần động của tải trọng gió phải được kể đến khi tính toán các công trình tháp, trụ, ống khói, cột điện, thiết bị dạng cột, hành lang băng tải, các giàn giá lộ thiên…, các nhà nhiều tầng cao hơn 40 mét, các khung ngang nhà công nghiệp một tầng một nhịp có độ cao trên 36 mét và tỉ số độ cao trên nhịp lớn hơn 1,5.
1.3. Đối với công trình cao và kết cấu mềm (ống khói, trụ, tháp,…) còn phải tiến hành kiểm tra mất ổn định khí động. Việc kiểm tra có thể tham khảo phần phụ lục C của chỉ dẫn này.
1.4. Đối với các công trình đặc thù thuộc các ngành: giao thông, thủy lợi, điện lực, bưu điện… cần chú ý đến các yêu cầu tính toán riêng cho phù hợp với đặc tính của từng loại công trình.
2. Nguyên tắc cơ bản
2.1. Tải trọng gió gồm hai phần: thành phần tĩnh và thành phần động. Giá trị và phương tính toán của thành phần tĩnh tải trọng gió được xác định theo các điều khoản ghi trong tiêu chuẩn tải trọng và tác động TCVN 2737 : 1995 [1].
Thành phần động của tải trọng gió được xác định theo các phương tương ứng với phương tính toán thành phần tĩnh của tải trọng gió.
2.2. Thành phần động của tải trọng gió tác động lên công trình là lực do xung của vận tốc gió và lực quán tính của công trình gây ra. Giá trị của lực này được xác định trên cơ sở thành phần tĩnh của tải trọng gió nhân với các hệ số có kể đến ảnh hưởng của xung vận tốc gió và lực quán tính của công trình.
2.3. Việc tính toán công trình chịu tác dụng của động lực của tải trọng gió bao gồm: Xác định thành phần động của tải trọng gió và phản ứng của công trình do thành phần động của tải trọng gió gây ra ứng với từng dạng dao động.
2.4. Số hiệu của các công thức, các điều, mục, bảng biểu hoặc hình vẽ… được diễn giải hoặc quy định vận dụng trong nội dung của các điều, mục hoặc các phụ lục; nếu không ghi cụ thể các tài liệu kèm theo thì được hiểu là công thức, điều, mục, bảng biểu hoặc hình vẽ của chỉ dẫn này.
3. Trình tự các bước tính toán xác định thành phần động của tải trọng gió
3.1. Xác định xem công trình có thuộc phạm vi phải tính thành phần động và phải kiểm tra mất ổn định khí động học theo các điều 1.2 và 1.3 trong chỉ dẫn.
3.2. Thiết lập sơ đồ tính toán động lực
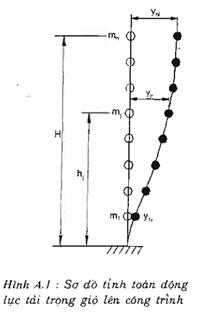
3.2.1. Sơ đồ tính toán được chọn là hệ thanh công xôn có hữu hạn điểm tập trung khối lượng, xem phụ lục A, hình A.1.
3.2.2. Chia công trình thành n phần sao cho mỗi phần có độ cứng và áp lực gió lên bề mặt công trình có thể coi như không đổi.
3.2.3. Vị trí của các điểm tập trung khối lượng đặt tương ứng với cao trình trọng tâm của các kết cấu truyền tải trọng ngang của công trình (sàn nhà, mặt bằng bố trí giằng ngang, sàn thao tác), hoặc trọng tâm của các kết cấu, các thiết bị cố định, các vật liệu chứa thường xuyên (nước trong các bầu đài của các tháp nước…).
3.2.4. Giá trị khối lượng tập trung ở các mức trong sơ đồ tính toán bằng tổng giá trị các khối lượng của kết cấu chịu lực, kết cấu bao che, trang trí, khối lượng của các thiết bị cố định (máy cắt, môtơ, thùng chứa, đường ống…), các vật liệu chứa (chất lỏng, vật liệu rời…) và các khối lượng khác. Việc tính toán, tổ hợp các khối lượng tập trung này phải tuân theo các quy định của TCVN 2737 : 1995 và các tiêu chuẩn có liên quan khác.
Khi kể đến các khối lượng chất tạm thời trên công trình trong việc tính toán động lực tải trọng gió, cần đưa vào hệ số chiết giảm khối lượng.
Bảng 1 – Hệ số chiết giảm đối với một số dạng khối lượng chất tạm thời trên công trình
|
Dạng khối lượng |
Hệ số chiết giảm khối lượng |
|
|
Bụi chất đống trên mái |
0,5 |
|
|
Các vật liệu chứa chất trong kho, silô, bunke, bể chứa |
1,0 |
|
|
Người, đồ đạc trên sàn tính tương đương phân bố đều |
Thư viện và các nhà chứa hàng, chứa hồ sơ |
0,8 |
|
Các công trình dân dụng khác |
0,5 |
|
|
Cầu trục và cầu treo các vật nặng |
Có móc cứng |
0,3 |
|
Có móc mềm |
0,0 |
|
3.2.5. Độ cứng của thanh công xôn lấy bằng độ cứng tương đương của công trình. Có thể xác định độ cứng tương đương trên cơ sở tính toán sao cho sự chuyển dịch ở đỉnh của công trình thực và ở đỉnh của thanh công xôn là bằng nhau khi tác dụng tại đỉnh công trình và đỉnh thanh công xôn cùng một lực ngang.
3.3. Xác định giá trị tiêu chuẩn thành phần tĩnh của áp lực gió lên các phần của công trình
3.3.1. Xác định áp lực gió tiêu chuẩn theo điều 4.11.
3.3.2. Xác định hệ số cao k(zj) đối với từng phần thứ j của công trình theo bảng 7, trong đó xác định mốc chuẩn để tính độ cao xác định theo phụ lục A, mục A.2.3.
3.3.3. Xác định hệ số khí động c đối với từng phần của công trình theo bảng 6 của TCVN 2737 : 1995.
3.3.4. Xác định giá trị tiêu chuẩn thành phần tĩnh của áp lực gió lên các phần công trình, xác định theo điều 4.10.
3.4. Xác định giá trị tiêu chuẩn thành phần động của tải trọng gió tác dụng lên các phần tính toán của công trình, khi chỉ kể đến ảnh hưởng của xung vận tốc gió.
3.4.1. Xác định hệ số áp lực động và hệ số tương quan không gian đối với các phần tính toán của công trình theo bảng 3, bảng 4 và bảng 5.
3.4.2. Xác định giá trị tiêu chuẩn thành phần động của tải trọng gió tác dụng lên các phần tính toán của công trình, khi chỉ kể đến ảnh hưởng của xung vận tốc gió theo điều 4.2.
3.5. Xác định giá trị tiêu chuẩn và giá trị tính toán của thành phần động tải trọng gió lên các phần tính toán của công trình.
3.5.1. Xác định tần số và dạng dao động
3.5.1.1. Xác định tần số dao động thứ nhất f1 (Hz) của công trình. Có thể vận dụng các công thức trong phụ lục B, các điều từ B.1 đến B.3.
3.5.1.2. So sánh tần số f1 với tần số giới hạn fL trong bảng 2. Nếu f1 > fL thì giá trị tiêu chuẩn thành phần động của tải trọng gió lên các phần công trình được xác định theo điều 4.2. Nếu tần số f1 < fL thì giá trị tiêu chuẩn thành phần động của tải trọng gió được xác định theo điều từ 4.3 đến 4.8.
3.5.2. Xác định giá trị tính toán thành phần động của tải trọng gió lên các phần tính toán của công trình theo điều 4.9.
3.6. Tổ hợp nội lực và chuyển vị của công trình do thành phần tĩnh và động của tải trọng gió gây ra theo điều 4.12.
4. Xác định thành phần động của tải trọng gió theo TCVN 2737 : 1995.
4.1. Tùy thuộc mức độ nhạy cảm của công trình đối với tác dụng động lực của tải trọng gió mà thành phần động của tải trọng gió chỉ cần kể tác động do thành phần xung của vận tốc gió hoặc cả với lực quán tính của công trình.
Mức độ nhạy cảm được đánh giá qua tương quan giữa giá trị các tần số dao động riêng cơ bản của công trình, đặt biệt là tần số dao động riêng thứ nhất, với tần số giới hạn fL có trong bảng 2. Các giá trị cho trong bảng này lấy theo TCVN 2737 : 1995.
Bảng 2 – Giá trị giới hạn của tần số dao động riêng fL.
|
Vùng áp lực gió |
fL (Hz) |
|
|
d = 0,3 |
d = 0,15 |
|
|
I II III IV V |
1,1 1,3 1,6 1,7 1,9 |
3,4 4,1 5,0 5,6 5,9 |
Chú thích : d - Là độ giảm loga dao động của kết cấu, phụ thuộc vào dạng kết cấu và vật liệu chị lực chính của công trình. Theo TCVN 2737 : 1995, các giá trị của d cho trong bảng 2 tương ứng với dạng công trình ghi trong phần chính của hình 2.
4.2. Đối với công trình và các bộ phận kết cấu có tần số dao động cơ bản f1 (Hz) lớn hơn giá trị giới hạn của tần số dao động riêng fL quy định trong điều 4.1, thành phần dao động của tải trọng gió chỉ cần kể đến tác dụng của xung vận tốc gió. Khi đó giá trị tiêu chuẩn thành phần động của áp lực gió Wpj tác dụng lên phần thứ j của công trình được xác định theo công thức:
Wpj = Wj zjv (4.1)
Trong đó:
Wpj – áp lực, đơn vị tính toán là daN/m2 hoặc kN/m2 tùy theo đơn vị tính toán của Wj ;
Wj – là giá trị tiêu chuẩn thành phần tĩnh của áp lực gió, tác dụng lên phần thứ j của công trình, xác định theo điều 4.10 ;
zj – là hệ số áp lực động của tải trọng gió, ở độ cao tương ứng với phần thứ j của công trình, không thứ nguyên. Các giá trị của zj lấy theo TCVN 2737 : 1995 và được cho trong bảng 3.
v – hệ số tương quan không gian áp lực động của tải trọng gió ứng với các dạng dao động khác nhau của công trình, không thứ nguyên. Trong công thức (4.1), v được lấy bằng v1. Nếu bề mặt đón gió của công trình có dạng chữ nhật định hướng song song với các trục cơ bản trong hình 1 thì các giá trị của v1 lấy theo bảng 4, trong đó các tham số p và % xác định theo bảng 5, giá trị của v ứng với dạng dao động thứ 2 và thứ 3 là v2 = v3 = 1. Các giá trị trong bảng 4 và bảng 5 lấy theo TCVN 2737 : 1995.
Bảng 3 – Hệ số áp lực động z
|
Chiều cao z (m) |
Hệ số áp lực động z đối với các dạng địa hình |
||
|
A |
B |
C |
|
|
≤ 5 10 20 40 60 80 100 150 200 250 300 350 ³ 480 |
0,318 0,303 0,289 0,275 0,267 0,262 0,258 0,251 0,246 0,242 0,239 0,236 0,231 |
0,517 0,486 0,457 0,429 0,414 0,403 0,395 0,381 0,371 0,364 0,358 0,353 0,343 |
0,754 0,684 0,621 0,563 0,532 0,511 0,496 0,468 0,450 0,436 0,455 0,416 0,398 |
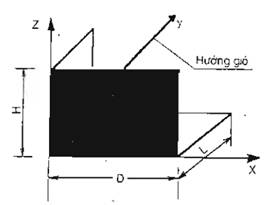
Hình 1 : Hệ tọa độ khi xác định hệ số tương quan không gian v.
Bảng 4 – Hệ số tương quan không gian v1 khi xét tương quan xung vận tốc gió theo chiều cao và bề rộng đón gió, phụ thuộc vào p và %
|
p(m) |
Hệ số v1 khi g bằng (m) |
||||||
|
5 |
10 |
20 |
40 |
80 |
160 |
350 |
|
|
0,1 5 10 20 40 80 160 |
0,95 0,89 0,85 0,80 0,72 0,63 0,53 |
0,92 0,87 0,84 0,78 0,72 0,63 0,53 |
0,86 0,84 0,81 0,76 0,70 0,61 0,52 |
0,83 0,80 0,77 0,73 0,67 0,59 0,50 |
0,76 0,73 0,71 0,68 0,63 0,56 0,47 |
0,67 0,65 0,64 0,61 0,57 0,51 0,44 |
0,56 0,54 0,53 0,51 0,48 0,44 0,38 |
Bảng 5 – Các tham số p và %
|
Mặt phẳng tọa độ cơ ban song song với bề mặt tính toán |
p |
X |
|
zox zoy xoy |
D 0,4L D |
H H L |
Chú thích : Đối với công trình có bề mặt đón gió không phải là hình chữ nhật thì H lấy bằng chiều cao công trình còn D và L lấy bằng kích thước tương ứng tại trọng tâm hình chiếu của bề mặt đón gió lên các mặt phẳng thẳng đứng, vuông góc với phương luồng gió.
4.3. Đối với công trình và các bộ phận kết cấu có tần số dao động cơ bản f1 (Hz) nhỏ hơn giá trị giới hạn của tần số dao động riêng fL quy định trong điều 4.1 thì thành phần động của tải trọng gió phải kể đến tác dụng của cả xung vận tốc gió và lực quán tính của công trình. Khi đó, số dạng dao động cần tính toán và giá trị tiêu chuẩn thành phần động của tải trọng gió Wp(ji) tác dụng lên phần thứ j của công trình ứng với dạng dao động thứ i được xác định theo các điều từ 4.4 đến 4.8.
4.4. Các công trình hoặc bộ phận kết cấu có tần số dao động riêng cơ bản thứ s, thỏa mãn bất đẳng thức :
...
thì cần tính toán thành phần động của tải trọng gió với s dạng dao động đầu tiên.
4.5. Giá trị tiêu chuẩn phần động của tải trọng gió tác dụng lên phần thứ j ứng với dạng dao động thứ i được xác định theo công thức :
![]()
Trong đó :
Wp(ji) - lực, đơn vị tính toán thường lấy là daN hoặc kN tùy theo đơn vị tính toán của W trong công thức tính hệ số yi ;
Mj – khối lượng tập trung của phần công trình thứ j, (t) ;
xi – hệ số động lực ứng với dạng dao động thứ i, không thứ nguyên, phụ thuộc và thông số e1 và độ giảm lôga của dao động :
![]()
Trong đó :
y – hệ số độ tin cậy của tải trọng gió, lấy bằng 1,2 ;
Wn – giá trị của áp lực gió (N/m2) ;
fi – tần số dao động riêng thứ i (Hz).
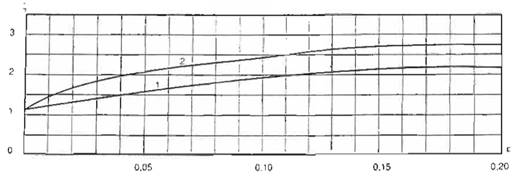
Hình 2 : Đồ thị xác định hệ số động lực
Chú thích:
1) Đường cong 1 – Sử dụng cho các công trình bê tông thép và gạch đá kể cả các công trình bằng khung thép có kết cấu bao che (d = 0,3).
2) Đường cong 2 – Sử dụng cho các công trình tháp, trụ thép, ống khói, các thiết bị dạng cột có bệ bằng bêtông cốt thép ((d = 0,15).
Yji – dịch chuyển ngang tỷ đối của trọng tâm phần công trình thứ j ứng với dạng dao động riêng thứ i, không thứ nguyên ;
y1 – hệ số được xác định bằng cách chia công trình thành n phần, trong phạm vi mỗi phần tải trọng gió có thể coi như là không đổi :

Trong đó :
WF) – giá trị tiêu chuẩn thành phần động của tải trọng gió tác dụng lên phần thứ j của công trình ứng với các dạng dao động khác nhau khi chỉ kể đến ảnh hưởng của xung vận tốc gió, có thứ nguyên là lực, xác định theo công thức :
![]()
Trong đó :
Wj, zi có nghĩa như trong công thức (4.1) ;
v – có ý nghĩa như trong công thức (4.1). Khi tính toán đối với dạng dao động thứ nhất, v lấy bằng v1, còn đối với các dạng dao động còn lại, v lấy bằng 1. Các giá trị của v1 được xác định như ở điều 4.2 ;
Sj – diện tích đón gió của phần j của công trình (m2) ;
Chú thích : Công thức (4.6) tương ứng với công thức 8 trong TCVN 2737 : 1995 nhưng được nhân thêm với Sj để chuyển kết quả tính từ áp lực thành lực.
4.6. Nhà có mặt bằng đối xứng có f1 < fL, thì ảnh hưởng của dạng dao động thứ nhất đến giá trị thành phần dao động của tải trọng gió là chủ yếu. Khi đó có thể xác định giá trị tiêu chuẩn thành phần động của tải trọng gió theo công thức :
![]()
Trong đó :
Wp(jj) – lực, có đơn vị tính toán phù hợp với đơn vị tính toán của WFj khi tính hệ số y1 ;
Mj, xj, yl- có ý nghĩa giống như trong công thức (4.3) nhưng với i = l ;
yjl – là dịch chuyển ngang tỉ đối của trọng tâm phần thứ j ứng với dạng dao động riêng thứ nhất. Cho phép lấy yjl bằng dịch chuyển đo tải trọng ngang phân bố đều đặt tĩnh gây ra.
4.7. Đối với nhà nhiều tầng có mặt bằng đối xứng, độ cứng, khối lượng và bề rộng mặt đón gió không đổi theo cao, có fl < f L cho phép xác định giá trị tiêu chuẩn thành phần động của áp lực gió ở độ cao z theo công thức :
![]()
Trong đó :
WFz – áp lực, có đơn vị tính toán phù hợp với đơn vị tính toán của WpH ;
x - hệ số động lực ứng với dạng dao động cơ bản của công trình ;
WpH – giá trị tiêu chuẩn thành phần động của áp lực gió ở độ cao H của đỉnh công trình, xác định theo công thức (4.1).
4.8. Đối với công trình hoặc các bộ phận kết cấu mà sơ đồ tính toán có dạng một bậc tự do và có fI < fL, giá trị tiêu chuẩn thành phần động của áp lực của gió được xác định theo công thức :
![]()
Trong đó :
Wp, W – giá trị tiêu chuẩn thành phần động và thành phần tĩnh của áp lực gió ứng với độ cao tính toán, có thứ nguyên là lực trên diện tích ;
z - là hệ số áp lực động của tải trọng gió, không thứ nguyên ;
x ,v - là hệ số động lực và hệ số tương quan không gian áp lực động ứng với dạng dao động cơ bản, không thứ nguyên.
4.9. Giá trị tính toán thành phần động của tải trọng hoặc áp lực gió được xác định theo công thức:
![]()
Trong đó :
Wu – là giá trị tính toán của tải trọng gió hoặc áp lực gió ;
W – là giá trị tiêu chuẩn của tải trọng gió hoặc áp lực gió, xác định theo các công thức (4.1), (4.3), (4.8), (4.9);
g – là hệ số độ tin cậy đối với tải trọng gió, y lấy bằng 1,2.
b - là hệ số điều chỉnh tải trọng gió theo thời gian sử dụng giả định của công trình, xác định theo bảng 6. Các giá trị cho trong bảng này lấy theo TCVN 2737 :1995.
Bảng 6: Hệ số b
|
Thời gian sử dụng giả định |
5 |
10 |
20 |
30 |
40 |
50 |
|
Hệ số điều chỉnh tải trọng gió b |
0,61 |
0,72 |
0,83 |
0,91 |
0,96 |
1,00 |
4.10. Giá trị tiêu chuẩn thành phần tĩnh của áp lực gió Wj tại điểm j ứng với độ cao zj so với mốc chuẩn xác định theo công thức [1] :
![]()
Trong đó :
Wj – có thứ nguyên là lực trên diện tích, tùy theo đơn vị tính toán của W ;
Wo – giá trị của áp lực gió tiêu chuẩn lấy theo phân vùng áp lực gió trong TCVN 2737 : 1995 ;
c – hệ số khí động lấy theo bảng 6 trong TCVN 2737 : 1995, không thứ nguyên ;
k(zj) – hệ số, không thứ nguyên, tính đến sự thay đổi của áp lực gió : k (zj) phụ thuộc vào độ cao zj, mốc chuẩn để tín độ cao và dạng địa hình tính toán. Các giá trị của k(zj) lấy theo TCVN 2737 : 1995, được cho trong bảng 7. Cách xác định mốc chuẩn đến tính độ cao xem phụ lục A, mục A.2.3.
Bảng 7: Hệ số k(zj) kể đến sự thay đổi áp lực gió theo độ cao và dạng địa hình
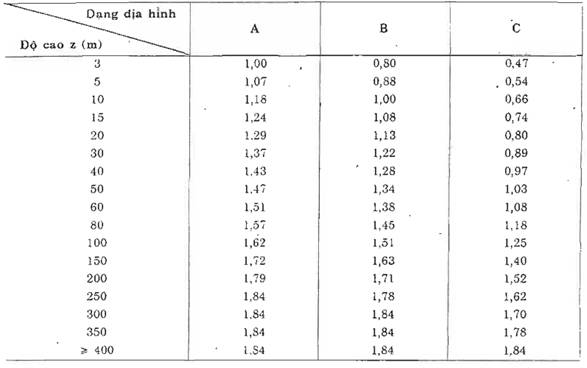
Chú thích :
1) Đối với độ cao trung gian, cho phép xác định giá k(zj) bằng cách nói suy tuyến theo bảng 7.
2) Khi xác định tải trọng gió cho một công trình, đối với các hướng gió khác nhau, có thể có các dạng địa hình khác nhau.
4.11. Giá trị của áp lực gió Wo được xác định từ vận tốc gió vo đã được xử lý trên cơ sở số liệu quan trắc vận tốc gió ở độ cao 10m so với mốc chuẩn (vận tốc trung bình trong khoảng thời gian 3 giây, bị vượt trung bình một lần trong 20 năm) ứng với địa hình phân vùng áp lực gió trong TCVN 2737 : 1995, cho trong bảng 8.
Đối với vùng ảnh hưởng của bão được đánh giá là yếu, giá trị của áp lực gió Wo được giảm đi 10daN/m2 đối với vùng I-A, 12daN/m2 đối với vùng II-A và 15daN/m2 đối với vùng III-A.
Bảng 8 – Giá trị áp lực gió tiêu chuẩn Wo
|
vùng áp lực gió |
I |
II |
III |
IV |
V |
|
Wo (daN/m2) |
65 |
95 |
125 |
155 |
185 |
Đối với vùng I, giá trị của áp lực gió Wo lấy theo bảng 8 được áp dụng để thiết kế nhà và công trình xây dựng ở vùng núi đồi, vùng đồng bằng và các thung lũng.
Những nơi có địa hình phức tạp (hẻm núi, giữa hai dãy núi song song, các cửa đèo…), giá trị của áp lực gió Wo phải lấy của Tổng cục Khí tượng thủy văn hoặc kết quả khảo sát hiện trường xây dựng dã được xử lý có kể đến kinh nghiệm sử dụng công trình. Khi đó, giá trị của áp lực gió Wo xác định theo công thức :
![]()
Chú thích : Trong công thức (4.12), vo được tính bằng m/s, còn Wo tính bằng daN/m2.
Nhà và công trình xây dựng ở vùng núi và hải đảo có cùng độ cao, cùng dạng địa hình và ở sát cạnh các trạm quan trắc khí tượng cho trong phụ lục F của TCVN 2737 : 1995 thì giá trị áp lực gió tính toán với thời gian giả định khác nhau được lấy theo trị số độc lập của các trạm này (xem bảng F1 và F2, phụ lục F trong TCVN 2737 : 1995).
4.12. Nội lực và chuyển vị gây ra do thành phần tĩnh và động của tải trọng gió được xác định như sau :
![]()
Trong đó :
X – là mômen uốn (xoắn), lực cắt, lực dọc, hoặc chuyển vị ;
X1 – là mômen uốn (xoắn), lực cắt, lực dọc hoặc chuyển vị do thành phần tĩnh của tải trọng gió gây ra ;
![]() – là mômen uốn
(xoắn), lực cắt, lực dọc hoặc chuyển vị do thành phần động của tải trọng gió gây
ra khi dao động ở dạng thứ i :
– là mômen uốn
(xoắn), lực cắt, lực dọc hoặc chuyển vị do thành phần động của tải trọng gió gây
ra khi dao động ở dạng thứ i :
s – số dạng dao động tính toán.
PHỤ LỤC A
(Tham khảo)
THIẾT LẬP CÁC CÔNG THỨC TÍNH TOÁN THÀNH PHẦN ĐỘNG CỦA TẢI TRỌNG GIÓ
A.1. Phản ứng của công trình và thành phần động của tải trọng gió :
Phương trình vi phân tổng quát mô tả dao động của thanh công xôn có hữu hạn bậc tự do, khi bỏ qua trọng lượng của thanh:
![]()
Trong đó :
[M], [C], [K] – là ma trận khối lượng, ma trận cản, và ma trận độ cứng của hệ
..., U - là véc tơ gia tốc, vận tốc và dịch chuyển của những tọa độ xác định bậc tự do của hệ W’(t) – là véc tơ lực kích động đặt tại các tọa độ tương ứng.
Dùng phép biến đổi :
u = [f]p (A.2)
Phương trình (A.1), với những điều kiện : [M] là ma trận đường chéo : [C] và [K] là các ma trận đối xứng xác định dương thì có thể đưa về hệ phương trình vi phân độc lập :
![]()
Với yi là tỉ lệ cản của kết cấu ứng với dạng dao động thứ i:
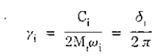
Trong đó : di – Độ giảm lôga của dạng dao động thứ i.
Đối với quá trình ngẫu nhiên dừng và hệ động lực tuyến tính không đổi theo thời gian thì từ (A.3), ứng với mỗi phương trình, ta có :
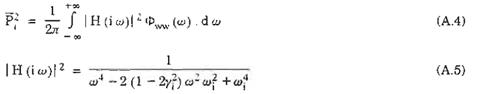
![]() - là giá trị trung
bình bình phương hiểu theo nghĩa xác suất của phản ứng Pi.
- là giá trị trung
bình bình phương hiểu theo nghĩa xác suất của phản ứng Pi.
fww (w) – là mật độ phổ của hàm tuơng quan tải trọng. Theo [6], fww (w) được xác định theo công thức:
![]()
Trong đó:
Fki, Fji - là dịch chuyển ngang tỉ đối ứng với dạng dao động chuẩn thứ i tại điểm k và điểm j;
Wk, Wj - là giá trị tiêu chuẩn thành phần tĩnh của tải trọng gió đặt tại điểm k và j;
xk, xj - là hệ số áp lực động của vận tốc gió, ứng với cao trình điểm k và j,
Sv (w) - là mật độ phổ tương hỗ của xung dọc vận tốc gió ở điểm k và j, được xác định theo công thức thực nghiệm của Davenport [6];
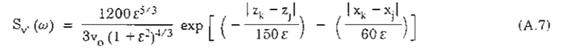
Từ (A.5) suy ra:
![]()
Trong đó:
![]()
Từ (A.4), (A.6), (A.7) và (A.8) ta có:
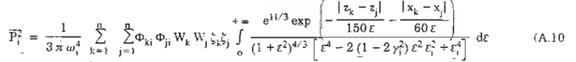
Khi không xét tương quan giữa các điểm k và j, ta có:
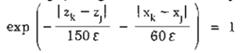
Khi đó ta có:
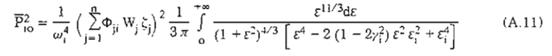
Đặt:
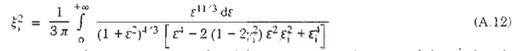
x1 - phụ thuộc vào ei tức là phụ thuộc vào tần số dao động riêng của công trình và cản của kết cấu, gọi là hệ số động lực. Dựa vào (A.12), lập được đồ thị xác định hệ số động lực
Ta có:
![]()
Suy ra:

Hay:

Trong đó:

vi - là hệ số tương quan không gian của xung dọc vận tốc gió
Công thức (A.15) là cơ sở để thiết lập công thức tính hệ số tương quan không gian của TCVN 2737 : 1995 trong mặt phẳng đón gió.
Từ (A.2) ta có chuyển vị tại điểm j:
![]()
Trong đó:

Với Mj – khối lượng ở điểm j;
yji - dịch chuyển ngang ti đối tại điểm j ở dạng dao động thứ i;
Từ (A.14), (A.16) và (A.17) ta có chuyển vị của công trình tại điểm j do thành phần động của tải trọng gió gây ra là:
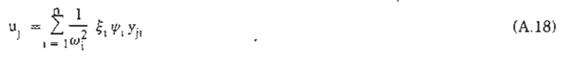
Hay:
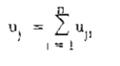
Trong đó:
uji - chuyển vị tại điểm j do thành phần động của tải trọng gió gây ra trong dạng dao động thứ i;

Theo định luật II Niutơn, ta có lực quán tính tác dụng lên điểm tập trung khối lượng Mj, ứng với dạng dao động thứ i là:
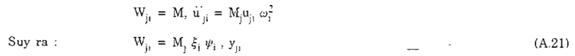
Công thức (A.21) là công thức để xác định thành phần động của tải trọng do tác dụng động lực của gió ứng với từng dạng dao động.
A.2. Hệ số độ cao k
A.2.1. Hệ số tính đến sự thay đổi của áp lực gió theo độ cao k được xác định trên cơ sở mô tả biến thiên vận tốc gió theo độ cao là hàm số mũ:
![]()
Trong đó:
ztg - là độ cao của địa hình dạng t mà ở đó vận tốc gió không còn chịu ảnh hưởng của mặt đệm, còn gọi là độ cao gradient;
Vt (z), Vtg - là vận tốc gió ở độ cao z và độ cao gradient của địa hình dạng t;
mt - là số mũ tương ứng với địa hình dạng t.
Các giá trị ztg, mt, ứng với t = A. B. C theo TCVN 2737 : 1995 cho trong bảng A.1.
Bảng A.1: Độ cao Gradient và hệ số mt
|
Dạng địa hình |
ztg (m) |
mt |
|
A B C |
250 300 400 |
0,070 0,090 0,140 |
Từ công thức (A.22) và các giá trị thực nghiệm cho trong Bảng A.1, có thể thiết lập được công thức xác định hệ số độ cao ứng với địa hình dạng t
![]()
Từ công thức (A.23), ta có bảng giá trị hệ số thay đổi áp lực gió theo độ cao trong TCVN 2737 : 1995.
A.2.2. Các dạng địa hình:
Theo TCVN 2737 : 1995 có 3 dạng địa hình sau:
- Địa hình dạng A là địa hình trống trải, không có hoặc có rất ít vật cản cao không quá 1.5m (bờ biển thoáng, mặt sông, hồ lớn, đồng muối, cánh đồng không có cây cao…).
- Địa hình dạng B là địa hình tương đối trống trải, có một số vật cản thưa thớt cao không quá 10m (vùng ngoại ô ít nhà, thị trấn, làng mạc, rừng thưa hoặc rừng non, vùng trồng cây thưa…).
- Địa hình dạng C là địa hình bị che chắn mạnh, có nhiều vật cản khác nhau cao từ 10m trở lên (trong thành phố, vừng rừng rậm…)
Công trình được xem là thuộc dạng địa hình nào nếu tính chất của dạng địa hình đó không thay đổi trong khoảng cách 30H khi H ≤ 60 mét và 2km khi H > 60m tính từ mặt đón gió của công trình. H là chiều cao của công trình.
A.2.3. Khi xác định hệ số k trong bảng 7, nếu mặt đất xung quanh nhà không bằng phẳng thì mốc chuẩn để tính độ cao z được xác định như sau:
a) Trường hợp mặt đất có độ dốc nhỏ so với phương nằm ngang: i ≤ 0,3; độ cao z được kể từ mặt đất đặt nhà và công trình tới điểm cần xét.
b) Trường hợp mặt đất có độ dốc 0,3 < i < 2, độ cao z được kể từ cao trình quy ước zo thấp hơn mặt đất thực tới đến điểm cần xét.
Mặt cao trình quy ước zo được xác định theo hình A.2.
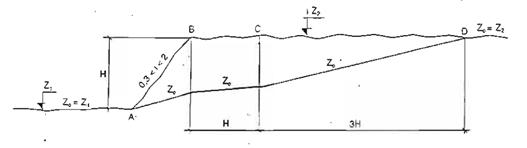
Hình A.2 : Cao trình zo khi 0,3 < i < 2.
Bên trái điểm A : zo = z1
Trên đoạn BC : zo = H(2-i)/1,7.
Bên phải điểm D : zo = z2
Trên đoạn AB và CD : Xác định zo bằng phương pháp nội suy tuyến tính.
c) Trường hợp mặt đất có độ dốc i ≥ 2 mặt cao trình quy ước zo để tính độ cao z thấp hơn mặt đất thực được xác định theo hình A.3.
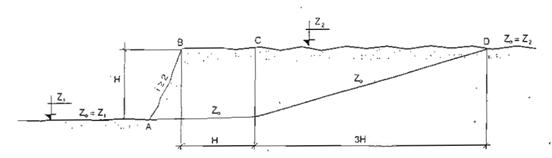
Hình A.3 : Cao trình zo khi i ≥ 2.
Bên trái điểm A : zo = z1
Bên phải điểm D : zo = z2
Trên đoạn CD : Xác định zo bằng phương pháp nội suy tuyến tính.
A.3. Hệ số áp lực động của tải trọng gió x :
Áp lực gió tác dụng lên công trình có độ cao z:
W(z,t) = W(z) + W’(z,t)
Trong đó:
W(z,t) - là áp lực của gió tác dụng lên công trình theo phương tác động của gió:
W(z) - là áp lực do thành phần trung bình của vận tốc gió, xác định theo công thức:
W(z) = 0.0613v2(z)
W’(z,t) - là áp lực do thành phần xung của vận tốc gió gây ra ở cùng độ cao z, được xác định theo công thức:
![]()
Trong đó:
V(z) - là thành phần trung bình của vận tốc gió ở độ cao z;
V'(z,t) - là thành phần xung của vận tốc gió ở cùng độ cao z.
Mức độ ảnh hưởng của thành phần xung của vận tốc gió lên công trình được đặc trưng bởi cường độ rối của dòng gió g*(…). Với một dạng địa hình xác định, ta có:
![]()
Trong đó:
g* (z) - là cường độ rối của dòng gió;
dv(z) - là trung bình bình phương thành phần xung dọc vận tốc gió ở độ cao z;
v(z) - là giá trị thành phần trung bình vận tốc gió ở độ cao z.
Công thức (A.26) được lập dựa trên giả thiết:
- Thành phần xung của vận tốc gió trong khảo sát này được giả thiết bằng tích của một hàm ngẫu nhiên theo thời gian và một hàm theo tọa độ không gian (tọa độ z).
V'(z,t) = dv(z)j(t)
- Trung bình bình phương của hàm j (t) bằng đơn vị.
dj(t) = 1
Từ (A.25), (A.26) và (A.27) ta có:
W’(z,t) = 2W(z) g*t (z)j(t)
Theo Davenfort [6], cường độ dòng rối được xác định theo công thức:
![]()
Trong đó:
t = A, B, C - là các dạng địa hình, xác định theo điều A.2.2;
rt - là độ nhám mặt đệm của địa hình dạng t;
z - là độ cao tính toán;
mt - là số mũ ứng với địa hình dạng t.
Theo Davenfort [6], hệ số áp lực của tải trọng gió được xác định theo công thức:
![]()
Trong đó: ac là hệ số.
Trong TCVN 2737 : 1995, ứng với thời gian lấy trung bình vận tốc gió là 3 giây, hệ số áp lực động xác định theo công thức:

Trong đó:
a = 1,395
rA = 0,002; rB = 0,005; rC = 0,01
Từ (A.32) ta thiết lập được bảng hệ số áp lực động z trong TCVN 2737 : 1995.
A.4. Hệ số tương quan không gian v.
Từ (A.10) suy ra ![]() i,
được tính theo công thức:
i,
được tính theo công thức:
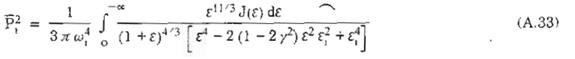
Trong đó:
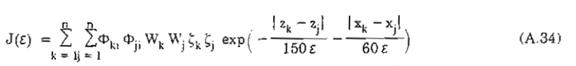
Xét công trình có khối lượng phân bố đều và độ cứng không thay đổi theo chiều cao. Dạng chuẩn của dao động riêng thứ nhất giả thiết có dạng:
![]()
Từ (A.23) suy ra:
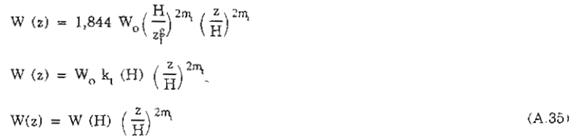
Từ (A.30) và (A.31) ta có:
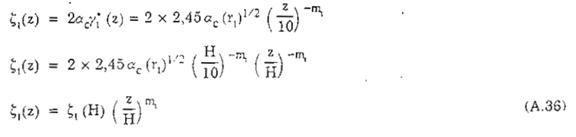
Trong đó:
W(z), W(H) – áp lực tiêu chuẩn do thành phần trung bình của vận tốc gió gây ra tại cao trình z và H;
xt(z); x(H) – hệ số áp lực động của địa hình dạng t ở độ cao z và H;
mt – số mũ ứng với địa hình dạng t lấy theo mục A.2.1.
Thay (A.35) và (A.36) vào (A.34) ta có:
![]()
Trong đó:
![]()
H – là chiều cao của công trình (m);
D – là bề rộng bề mặt đón gió của công trình (m).
Từ (A.37) suy ra:
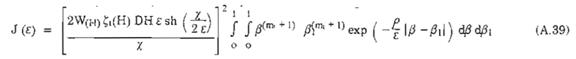
Khi không xét đến ảnh hưởng tương quan giữa các điểm k và j ta có:
![]()
Tương ứng khi đó, từ (A.39) suy ra:
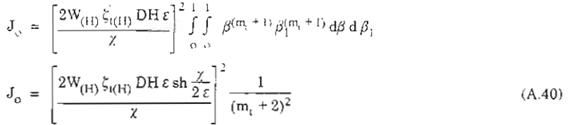
Từ (A.11), ta có
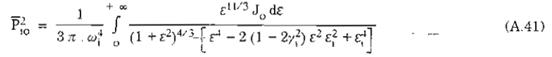
Hay
![]()
Từ (A.15), (A.33), (A.39), (A.40) và (A.42) ta có:
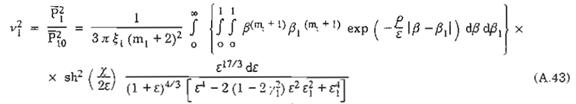
Nếu bỏ qua ảnh hưởng của tham số e1, mt, x1 và tỉ lệ cản y1 của kết cấu trong công thức (A.43), thì hệ số tương quan không gian v1 chỉ phụ thuộc vào các tham số p, y, là kích thước đặc trưng ở các bề mặt của công trình trên đó lấy tương quan không gian áp lực động của tải trọng gió. Từ công thức (A.43), ta xác định được bằng giá trị của hệ v1 trong TCVN 2737 : 1995.
A.5. Hệ số động lực x:
Công thức (A.12) là cơ sở để thiết lập đồ thị xác định hệ số động lực xt trong TCVN 2737 : 1995, trong đó xt phụ thuộc vào thông số ei và cản của kết cấu, tức là phụ thuộc vào tần số f1 và độ giảm lôga của dao động d
PHỤ LỤC B
(tham khảo)
XÁC ĐỊNH CÁC ĐẶC TRƯNG CỦA ĐỘNG LỰC
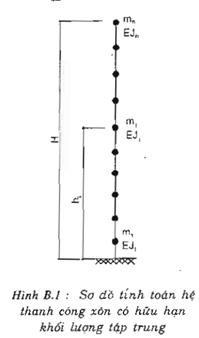
B.1. Xác định tần số và dạng dao động của hệ kết cấu dạng thanh công xôn có hữu hạn khối lượng tập trung:
Xét hệ gồm một thanh công xôn, có n điểm tập trung khối lượng, hình B.1. Phương trình vi phân tổng quát mô tả dao động của hệ số khi bỏ qua trọng lượng của thanh có dạng (A.1).
Tần số và dạng dao động riêng được xác định từ phương trình vi phân thuần nhất không có cản:
MU + KU = 0 (B.1)
Đặt U = y sin (wt - a) (B.2)
Từ (B.1) và (B.2) ta có:
![]()
Trong đó:
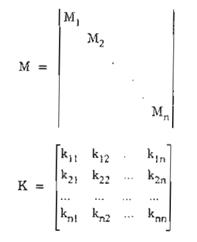
Với:
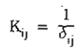
Điều kiện tồn tại dao động: y = 0, suy ra:
K = w2 M = 0 (B.4)
Hay:
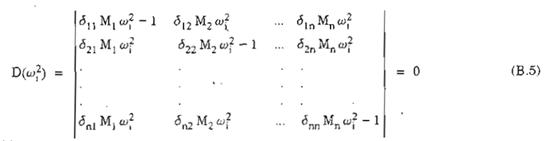
Trong đó:
Mj – là khối lượng tập trung ở điểm thứ j;
dji – là chuyển vị tại điểm j do lực đơn vị đặt tại điểm i gây ra;
w1 – là tần số vòng của dao động riêng (Rad/s).
Phương trình (B.5) gọi là phương trình đặc trưng. Từ (B.5) có thể xác định được n giá trị thực, dương của wi. Thay các giá trị wi tìm được vào phương trình (B.3) sẽ xác định được các dạng dao động riêng. Khi số điểm tập trung khối lượng n > 4, phương trình (B.5) chỉ có thể tìm được nghiệm gần đúng và phải thông qua một khối lượng tính toán lớn và phức tạp. Khi đó tần số và dạng dao động được xác định bằng cách giải trên máy tính nhờ các chương trình
Dưới đây là một số công thức để xác định tần số và dạng dao động riêng.
B.1.1. Công trình có sơ đồ tính toán là thanh công xôn có một khối lượng tập trung.
- Phương trình đặc trưng có dạng
![]()
- Tần số dao động riêng xác định từ công thức

Thứ nguyên của w là Rad/s, còn thứ nguyên của f là 1/s hay Hz.
Trường hợp công trình có độ cứng EJ không đổi và liên kết ngàm ở móng:
![]()
Với H là chiều cao công trình (m).
Thay (B.9) vào (B.8) ta có tần số dao động riêng:
![]()
B.1.2. Công trình có sơ đồ tính toán là thanh công xôn có hai khối lượng tập trung.
- Phương trình đặc trưng có dạng:
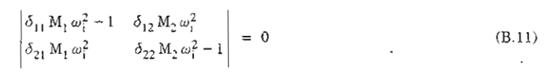
Hay:
![]()
- Tần số dao động riêng xác định từ công thức:

Trong đó:

- Các dạng dao động riêng xác định được từ phương trình:
![]()
Trong đó:
wi - được xác định từ (B.13)
yit – chọn trước bằng một giá trị nào đó, thường lấy yit = 1.
B.1.3. Công trình có sơ đồ tính toán là thanh công xôn có ba khối lượng tập trung.
- Phương trình đặc trưng có dạng:
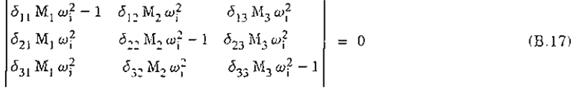
Hay:
![]()
Trong đó:
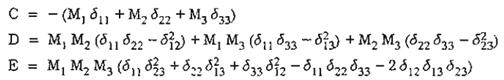
Từ phương trình (B.18) sẽ xác định được 3 nghiệm thực dương ứng với 3 tần số dao động riêng.
- Các dạng dao động riêng xác định được từ phương trình:
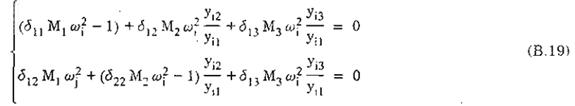
Trong đó: yi1 chọn trước bằng một giá trị nào đó, thường lấy yi1 = 1.
B.1.4. Công trình có sơ đồ tính toán là thanh công xôn có n khối lượng tập trung.
- Trường hợp n > 4, có thể xác định tần số dao động riêng từ bất đẳng thức kép:
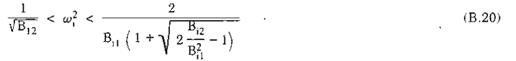
Khi xác định tần số dao động riêng thứ nhất (i = 1), giá trị B11, B12 lấy bằng:
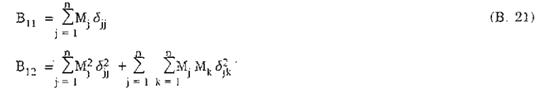
Khi xác định tần số dao động riêng thứ hai (i = 2), giá trị B21, B22 lấy bằng:

- các dạng dao động riêng xác định từ hệ phương trình:
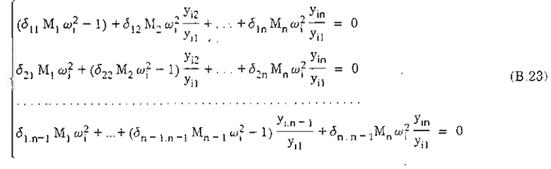
Trong đó: yi1 thường lấy bằng đơn vị.
B.2. Công trình có sơ đồ tính toán là thanh công xôn có khối lượng phân bố đều.
B.2.1. Đối với các công trình có khối lượng phân bố đều (m), độ cứng EJ không đổi và liên kết ngàm ở đáy thì tần số dao động riêng được xác định theo công thức [3.6].
![]()
Các tung độ của ba dạng dao động đầu tiên cho trong Bảng B.1 hoặc xác định theo công thức [3.6].
![]()
Trong các công thức (B.24) và (B.25), các hệ số ai và Bi tương ứng với 3 dạng dao động đầu tiên lấy bằng:
a1 = 1,875 B1 = 1,635
a2 = 4,694 B2 = 0,980
a3 = 7,860 B3 = 1,000
![]()
Trong đó:
fi - là tần số dao động riêng thứ i (Hz);
q - là trọng lượng đơn vị dài theo chiều cao công trình (kN/m);
EJ - là độ cứng chống uốn của công trình (kN.m2);
g - là gia tốc trọng trường (m/s2);
hj - là chiều cao của điểm khối lượng thứ j (m);
H- là chiều cao của toàn bộ công trình (m).
Bảng B.1. Giá trị các dịch chuyển ngang tỉ đối ứng với 3 dạng ao động đầu tiên của hệ có khối lượng phân bố đều và độ cứng không đổi.
|
x ti |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
1 |
0 |
0,017 |
0,064 |
0,136 |
0,230 |
0,340 |
0,462 |
0,558 |
0,725 |
0,863 |
1 |
|
2 |
0 |
0,093 |
0,301 |
0,526 |
0,685 |
0,715 |
0,589 |
0,317 |
0,007 |
-0,528 |
-1 |
|
3 |
0 |
0,224 |
0,605 |
0,957 |
0,526 |
0,020 |
-0,474 |
-0,658 |
-0,395 |
0,228 |
1 |
B.2.2. Nếu ngoài khối lượng phân bố đều, công trình còn có các khối lượng tập trung, thì có thể sử dụng công thức (B.24) để xác định các tần số dao động riêng nhưng khi đó q được lấy bằng trọng lượng phân bố đều quy đổi [3,6]:
![]()
Trong đó:
q' - trọng lượng phân bố đều (kN/m);
Pj - trọng lượng tập trung thứ j (kN);
yji - xác định theo công thức (B.25), không thứ nguyên;
n - số khối lượng tập trung;
l - là hệ số phụ thuộc vào dạng dao động riêng;
H - là chiều cao công trình (m).
Với 3 dạng dao động đầu tiên, giá trị của l lần lượt là:
l1 = 0,54 l2 = 1,04; l3 = 1;
B.2.3. Đối với công trình có tiết diện thay đổi theo chiều cao, tần số dao động riêng thứ nhất có thể xác định theo công thức [6]
Trong đó:
yH, yj - là chuyển vị ở đỉnh và trọng tâm của đoạn thứ j của công trình do lực P = 1kN đặt ở đỉnh công trình gây ra (m);
Pj - trọng lượng của đoạn công trình thứ j (kN);
n - số đoạn công trình;
g - gia tốc trọng trường (m/s2).
B.2.4. Đối với công trình dạng ống khói hoặc các công trình tương tự có mặt cắt ngang hình vành khuyên, tần số dao động riêng có kể đến ảnh hưởng biến dạng của nền, được xác định theo công thức [3.4.6].

Trong đó:
fi - là tần số dao động riêng thứ i (Hz);
E - là mô đun đàn hồi của vật liệu làm thân ống khói (kN/m2);
H - là chiều cao của ống khói từ đỉnh đến móng (m);
g - là gia tốc trọng trường (m/s2);
q - là trọng lượng thể tích của thân ống khói (kN/m3);
ro - là bán kính quán tính của tiết diện đáy ống khói (m).
![]()
Jo, Fo - là mô men quán tính và diện tích tiết diện đáy ống khói (m4, m2)
lI - là hệ số, ứng với dạng dao động thứ i. Với 3 dạng dao động đầu tiên, li được xác định theo các đồ thị hình B.2.
Lớp lót ống khói thường chỉ làm tăng trọng lượng còn hầu như không ảnh hưởng đến độ cứng của ống khói, khi đó giá trị q được tính gần đúng theo công thức:
![]()
Trong đó:
qth và qL - là trọng lượng thể tích của vật liệu làm thân ống khói và lớp lót (kN/m3)
Fth và FL - diện tích tiết diện ngang của phần thân và phần lớp lót ứng với độ cao trung bình của ống khói (m2).
Các dạng dao động riêng của ống khói được xác định theo công thức [3,4,6].
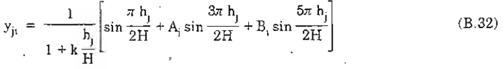
Trong đó:
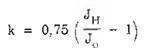
Ai, Bi - là các hệ số ứng với các dạng dao động riêng, được xác định theo các biểu đồ hình B.3.
Các hệ số li, Ai, Bi đối với mỗi dạng dao động phụ thuộc vào các tham số:
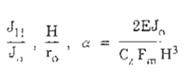
Trong đó:
JH, Jo - là mô men quán tính của tiết diện đỉnh và đáy ống khói (m4);
E - là mô đun đàn hồi của vật liệu làm thân ống khói (kN/m2);
hj - chiều cao từ đáy ống khói đến điểm đang xét (m);
Fm - diện tích đế móng ống khói (m2);
CL - hệ số nền của đất (kN/m2).
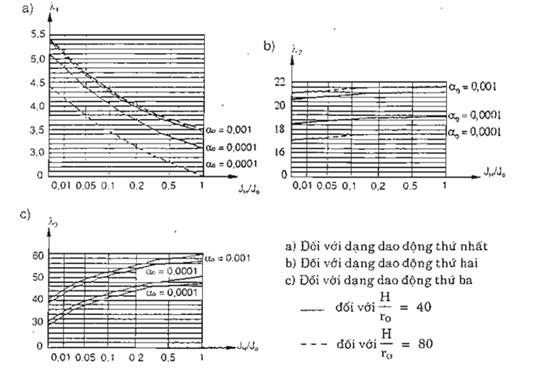
Hình B.2 – Biểu đồ xác định hệ số li
B.3. Một số công thức thực nghiệm ([3.6]
Chu kì dao động riêng cơ bản của các nhà có thể tính toán theo công thức thực nghiệm:
Công thức 1: T = a n (B.33)
Trong đó:
N - là số tầng nhà;
a - là hệ số phụ thuộc vào kết cấu của nhà và dạng nền. Đối với nền móng có biến dạng trung bình thì:
+ Nhà tấm lớn a = 0,047;
+ Nhà ở tường chịu lực bằng gạch đá và blốc lớn a = 0,056;
+ Nhà trường học và các công trình công cộng khác với tường chịu lực bằng gạch đá và blốc lớn = 0,065;
+ Khung bê tông cốt thép toàn khối, tường bằng gạch hoặc bê tông nhẹ = 0,064;
+ Khung thép chèn gạch hoặc bê tông nhẹ = 0,08.
Công thức 2:
![]()
Trong đó:
H - là chiều cao nhà tính bằng (m);
D - kích thước bề rộng mặt đón gió tính bằng (m);
µ - hệ số phụ thuộc vào dạng kết cấu:
+ Nhà có hệ thống chống gió bằng khung bê tông cốt thép µ = 0,09;
+ Nhà có hệ thống chống gió bằng khung thép µ = 0,10;
+ Nhà có hệ thống chống gió bằng tường xây gạch, đá hoặc bê tông thường
![]()
+ Nhà có hệ thống chống gió bằng tấm tường bê tông cốt thép
![]()
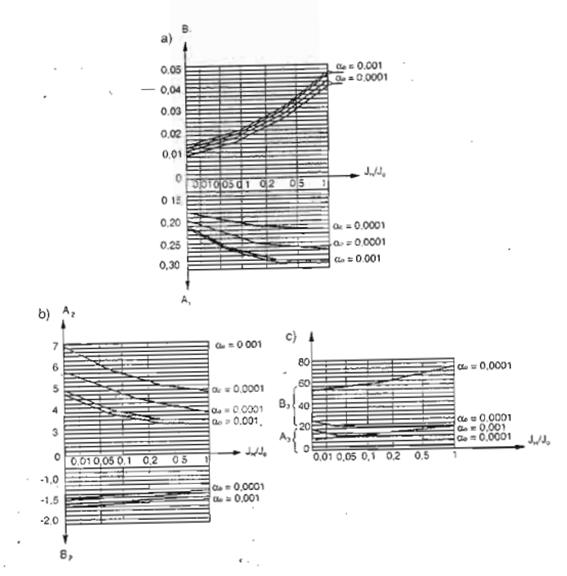
Hình B.3: Biểu đồ xác định hệ số Ai và Bi
a) Đối với dạng dao động thứ nhất;
b) Đối với dạng dao động thứ hai; c) Đối với dạng dao động thứ ba.
PHỤ LỤC C
(Tham khảo)
KIỂM TRA MẤT ỔN ĐỊNH KHÍ ĐỘNG CHO CÔNG TRÌNH CAO VÀ KẾT CẤU MỀM
C.1. Đặt vấn đề
Trong TCVN 2737 : 1995, điều 6.12 quy định: đối với các công trình cao và kết cấu mềm (ống khói, trụ, tháp…) cần phải kiểm tra mất ổn định khí động theo các chỉ dẫn riêng.
Dưới đây trình bày hiện tượng mất ổn định khí động và phương pháp tính toán, kiểm tra cho các công trình dạng trụ tròn và lăng trụ ứng với hai hiện tượng:
- Mất ổn định khí động do kích động xoáy đối với kết cấu và công trình dạng trụ tròn;
- Mất ổn định khí động galoping đối với kết cấu và công trình dạng lăng trụ.
C.2. Mất ổn định do kích động xoáy đối với kết cấu và công trình dạng trụ tròn:
C.2.1. Sự tách xoáy và lực khí động
Gió tạo nên phía sau công trình một dòng khí. Tính chất của dòng khí này phụ thuộc vào độ nhớt của nó mà đặc trưng là trị số Reynolds Rc:
Rc = 6900 vD (C.1)
Trong đó:
v - là vận tốc gió (ms);
D - là bề rộng mặt đón gió (m);
Rc - số Reynolds không thứ nguyên.
Các kết quả nghiên cứu [7, 8, 9, 10] cho thấy, đối với các công trình dạng trụ tròn khi:
· 3.102 ≤ Rc < 3.105 luồng khí phía sau công trình hình thành các xoáy có quy tắc và tách ra với chu kì xác định (hình C.1a) gọi là phạm vi gần tới hạn;
· 3.105 < Rc < 3,5.106 các xoáy phía sau công trình không theo quy tắc nào cả (hình C.1b) gọi là phạm vi trong giới hạn;
· Rc > 3,5.106 các xoáy dần trở lại và có quy tắc và tách ra với một chu kì xác định (hình C.1c) gọi là phạm vi vượt giới hạn.
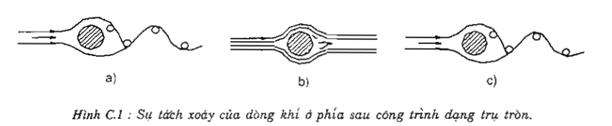
Dòng xoáy tách ra ở phía sau công trình tạo nên lực ngang làm công trình dao động theo phương vuông góc với luồng gió. Tùy theo tính chất tách xoáy có chu kì hay không có chu kì xác định mà dao động ngang của công trình và lực ngang tác dụng lên nó có tính tiền định hoặc ngẫu nhiên:
- Phạm vi gần tới hạn và vượt giới hạn, lực ngang có tính tiền định và tuần hoàn:
![]()
- Phạm vi trong giới hạn, lực ngang có tính ngẫu nhiên:
![]()
Trong đó:
P1 (z,t) - là lực ngang hướng gió tác dụng lên công trình ở cao độ z tại thời điểm t;
p (z) - là mật độ không khí ở độ cao z;
D(z) - là bề rộng diện tích đón gió ở độ cao z;
µL(z) - là hệ số lực ngang hướng gió ở độ cao z, xác định bằng thực nghiệm, µL (z) phụ thuộc vào Rc. Đối với công trình dạng trụ tròn quan hệ giữa µL (z) và Rc cho trong biểu đồ hình C.2 ;
f(t) – là hàm số ngẫu nhiên theo thời gian ;
wR – là tần số tách xoáy phía sau công trình, wR được xác định từ các công thức :

Với : Sh – số Struhal không thứ nguyên xác định bằng thực nghiệm, cho trong bảng C.1 ;
fR – tần số tách xoáy (Hz) ;
D(z) – bề rộng mặt đón gió (m), ở độ cao z ;
v – vận tốc gió (m/s) ;
Ts – chu kỳ tách xoáy phía sau công trình (s).
Các kết quả nghiên cứu [2] co thấy rằng : Khi vận tốc gió tăng thì tần số tách xoáy fs cũng tăng. Cho đến khi fs đạt đến f1 – là tần số dao động riêng của công trình thì xảy ra cộng hưởng dẫn đến công trình có thể bị mất ổn định khí động.
C.2.2. Vận tốc gió giới hạn và phạm vi tác dụng của lực khí động khi mất ổn định do kích động xoáy. Khoảng vận tốc gió làm cho tần số tách xoáy fs trùng với tần số dao động riêng fs của công trình gọi là khoảng vận tốc giới hạn. Theo chiều cao công trình, vận tốc gió thay đổi nên Rc cũng thay đổi theo. Vì vậy, một công trình tối đa có thể có ba phạm vi gắn tới hạn, trong giới hạn và vượt giới hạn (hình C.2). Khoảng vận tốc gió giới hạn gây mất ổn định dạng kích động xoáy có thể nằm trong phạm vi gần tới hạn hoặc phạm vi vượt giới hạn. Ở phạm vi vượt giới hạn thường vận tốc gió là lớn nên trong một số trường hợp, lực ngang hướng gió tác động lên công trình sẽ rất lớn gây mất ổn định khí động.
Vận tốc gió giới hạn nhỏ nhất sẽ ứng với trường hợp tần số tách xoáy fs trùng với tần số dao động riêng thứ nhất f1 của công trình, và được gọi là vận tốc gió tới hạn.
Từ quan hệ (C.4), ta có công thức để xác định vận tốc gió tới hạn.

Trong đó :
v* - là vận tốc gió tới hạn gây mất ổn định khi kích động xoáy ;
D(z), Sh – giống như trong công thức (C.4) ;
f1 – là tần số dao động riêng thứ nhất của công trình (Hz). Quan hệ giữa f1 và w1 được xác định theo công thức (C.5) với s = 1.
Kết quả nghiên cứu thực nghiệm [2] thấy rằng phạm vi xảy ra mất ổn định khí động do kích động xoáy nằm trong khoảng vận tốc gió :
![]()
Vận tốc gió theo độ cao thay đổi theo quy luật :
![]()
Trong đó :
![]() - là độ cao của
địa hình dạng t mà ở đó vận tốc gió không còn chịu ảnh hưởng của mặt đệm, còn
gọi là độ cao gradient ;
- là độ cao của
địa hình dạng t mà ở đó vận tốc gió không còn chịu ảnh hưởng của mặt đệm, còn
gọi là độ cao gradient ;
v1(z), ![]() -
là vận tốc gió ở độ cao z và độ cao gradient của địa hình dạng t ;
-
là vận tốc gió ở độ cao z và độ cao gradient của địa hình dạng t ;
mt – là số mũ tương ứng với địa hình dạng t, xác định bằng thực nghiệm.
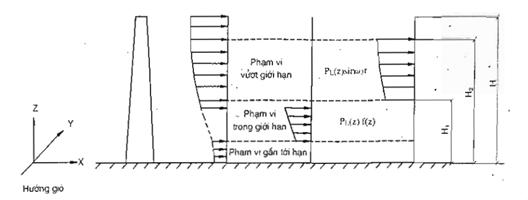
Hình C.2 : Các phạm vi tác dụng của lực ngay hướng gió lên công trình
Từ (C.7) và (C.8) ta có cao độ khởi đầu H1 và cao độ kết thúc H2 của khu vực cộng hưởng xác định theo công thức :

Trong đó :
v* – là vận tốc gió tới hạn (m/s) ;
vo – là vận tốc gió cơ bản ở độ cao 10 mét (m/s) ;
mt – là số mũ ứng với địa hình dạng t ;
1,3 – là hệ số xác định từ thực nghiệm.
Trường hợp H2 > H (H là chiều cao công trình) thì lấy H2 = H.
C.2.3. Chuyển vị và tải trọng tác dụng lên công trình khi mất ổn định dạng kích động xoáy ;
Nếu hướng gió theo phương y, ta có phương trình dao động của hệ
![]()
Trong đó
[M], [C], [K] – là các ma trận khối lượng, ma trận cản, và ma trận độ cứng của hệ theo phương vuông góc với luồng gió ;
…, X - là véc tơ gia tốc, vận tốc và dịch chuyển theo phương vuông góc với luồng gió của những tọa độ xác định khối lượng tập trung của hệ ;
F (t) – là vec tơ lực ngang hướng gió đặt tại các tọa độ tương ứng.
Dùng phép biến đổi : X= [j]q (C.11)
Trong đó [j] là ma trận biến đổi có tính trực quan với [M], [C], [K].
Bảng C.1 : Số struhat cho một số dạng mặt cắt

Thay (C.11), rút gọn ta có hệ phương trình vi phân tuyến tính
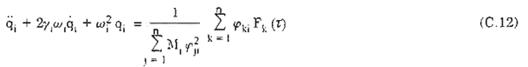
Trong đó : Fk (t) – là lực ngang hướng gió tác dụng lên điểm k
Nếu chỉ xét đến ảnh hưởng của lực cộng hưởng, ta có
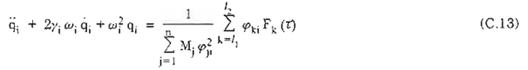
Trong đó :
![]()
l1 và l2 – là điểm thấp nhất và điểm cao nhất trong vùng cộng hưởng từ H1 và H2 ;
wk - là tần số tách xoáy ở phía sau công trình tại vùng cộng hưởng.
Thay (C.14) vào (C.13), ta có :
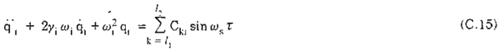
Với

Nghiệm của (C.15) có dạng :
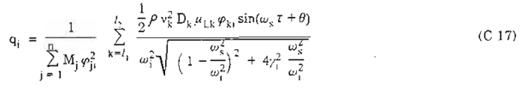
Trong đó :

Trường hợp cộng hưởng w1 = wS và vk = v'k, ta có:
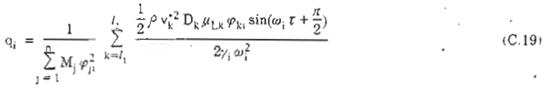
Suy ra :

![]() - là vận tốc gió
tới hạn ứng với cao trình điểm k
- là vận tốc gió
tới hạn ứng với cao trình điểm k
Từ (C.11) ta có :

Trong đó :
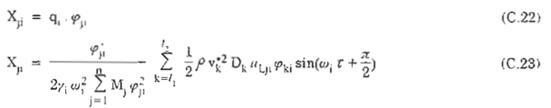
Từ (C.23) ta có chuyển vị lớn nhất tại điểm j của công trình ứng với dạng dao động thứ j khi xảy ra mất ổn định dạng kích động xoáy là :
![]()
Suy ra :
![]()
Trong đó : Mj – khối lượng tập trung tại điểm j
![]()
Với kết cấy thép gi = 0,02 ; kết cấu bê tông cốt thép gi = 0,05

Với :
p – là mật độ không khí (kN.s2/m4)
![]() - là vận tốc gió
tới hạn ở độ cao ứng với điểm k (m/s) ;
- là vận tốc gió
tới hạn ở độ cao ứng với điểm k (m/s) ;
Dk - là bề rộng đón gió của công trình ở độ cao ứng với điểm k (m) ;
jji, jki - là các dịch chuyển ngang tỉ đối với điểm j và điểm k ứng với dạng dao động thứ i.
mLk - là hệ số lực ngang hướng gió ở cao trình điểm k, lấy theo thực nghiệm, phụ thuộc vào trị số Reynolds Rc (hình C.3).
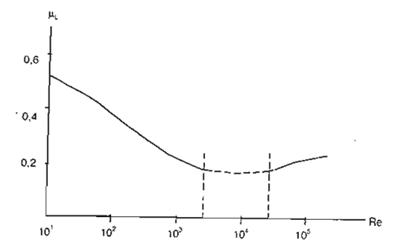
Hình C.3 : Quan hệ thực nghiệm Rc và µL của kết cấu ống tròn.
Dựa vào công thức (C.25), (C.26) ta có nhận xét : cản của kết cấu càng nhỏ, tải trọng do cộng hưởng gây nên càng lớn, nếu bỏ qua ảnh hưởng của cản kết cấu, tải trọng do cộng hưởng bằng vô cùng.
C.3. Mất ổn định khí động dạng galoping đối với kết cấu và công trình lăng trụ
C.3.1. Hiện tượng
Công trình phản ứng dưới tác dụng của tải trọng gió, thông thường do có cản kết cấu nên phản ứng bị khống chế, dao động sẽ ổn định, nhưng trong một số trường hợp nhất định, bộ phận kích động có thể sinh ra thành phần cản khí động. Nếu tốc độ gió đạt đến một trị nhất định nào đó mà giá trị của thành phần cản khí động lớn hơn giá trị cản của kết cấu, khi đó chấn động động sinh ra sẽ ngày một tăng cho đến cực đại và gây ra phá hoại do mất ổn định khí động (2, 5, 6), còn gọi là hiện tượng galoping. Vấn đề ở đây là thiết kế sao cho công trình không rơi vào trạng thái mất ổn định.
C.3.2. Phản ứng của công trình và vận tốc gió tới hạn
Xét mặt cắt ngang của vật thể hình lăng trụ có độ cứng và tiết diện không đổi chịu tác dụng của tải trọng gió (hình C.4).
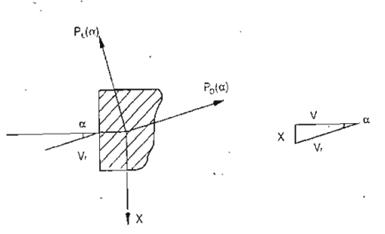
Hình C.4 : Lực tác dụng của gió lên vật thể lăng trụ.
Phương trình dao động ngang hướng gió
mx + cx + kx = Po (a) (C.28)
Trong đó :
m – là khối lượng phân bố ;
c – là hệ số cản của kết cấu theo phương ngang luồng gió ;
k – là độ cứng của hệ theo phương ngang luồng gió.
Chiếu các lực lên phương x, ta có :
Po (a) = -PD (a) sina - PL cosa (C.29)
Trong đó :
Po(a) – lực tác dụng lên vật hể theo phương ngang luồng gió ứng với góc tới a của gió ;
PD(a), PL(a) – lực tác dụng của gió lên vật thể ứng với góc tới a theo phương dọc và vuông góc với luồng gió :

µD(a), µL(a) – hệ số lực theo phương dọc và vuông góc với luồng gió ứng với góc tới a.
Thay (C.30) vào (C.29), ta có :
![]()
Vì
![]()
Nên
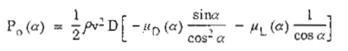
Hay
![]()
Trong đó
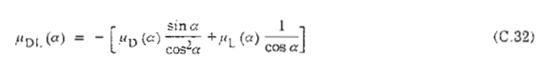
Với a nhỏ, ta có thể khai triển µDL (a) theo chuỗi Taylo tại a = 0 và lấy gần đúng với hai số hạng đầu của chuỗi.
![]()
Với a
= 0, suy ra ![]() , vì vậy ta có:
, vì vậy ta có:
![]()
Thay mDL (a) từ (C.33) vào (C.31) và thế vào Po (a) trong (C.28), rút gọn ta có:
![]() (C.34)
(C.34)
Trong đó :

Nghiệm của (C.34) có dạng:
![]()
x – là chuyển vị ngang luồng gió của tiết diện khảo sát ;
xo – là nghiệm riêng của phương trình (C.34) ;
b,q - là các hằng số tích phân.
Từ (C.37) ta thấy :
- Khi g > 0, biên độ dao động sẽ giảm dần, công trình trong trạng thái ổn định.
- khi g < 0, biên độ dao động tăng lên vô hạn theo t, công trình trong trạng thái mất ổn định.
- khi g = 0, công trình ở trạng thái tới hạn. Khi đó, từ (C.35) ta có điều kiện gây mất ổn định khí động dạng galoping là :

Trong đó:
v – là vận tốc gió tác dụng lên công trình (m/s) ;
v* – là vận tốc gió tới hạn (m/s) ;
p – là mật độ không khí (kN.s2/m4) ;
D – là bề rộng đón gió của công trình ở cao trình tính toán (m)
c – là hệ số cản của kết cấu theo phương ngang luồng gió.
Từ (C.28) và (C.34) ta có :
![]()
Trong đó :
w - Xác định từ công thức (C3.6) ;
m – Khối lượng phân bố của công trình (T/m) ;
g – Là tỉ cản của kết cấu theo phương ngang luồng gió ;
![]()
d - là độ giảm loga của dao động.
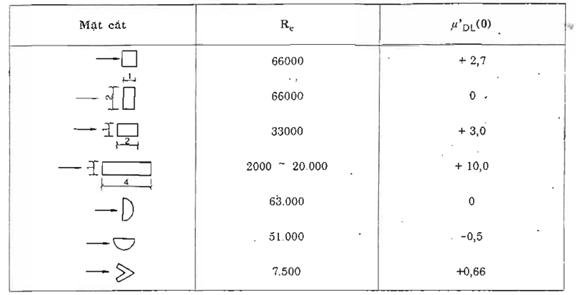
µDL (0) – được xác định bằng thực nghiệm. Ứng với các dạng tiết diện khác nhau, µDL (0) cho trong bảng C.2.
Công thức (C.38) dùng để kiểm tra khả năng mất ổn định khí động dạng galoping cho các công trình.
Thường hệ số cản của kết cấu c > 0, nên điều kiện để g < 0 là µDL (0) > 0.
Từ (C.32), ta có :
![]()
Vậy điều kiện cần để xảy ra mất ổn định khí động dạng galoping là :
![]()
Với kết cấu và công trình có tiết diện tròn ta có :
![]()
Mặt khác µD (a) > 0.
Vì vậy theo (C.41) thì kết cấu và công trình có tiết diện tròn không thể xảy ra mất ổn định khí động dạng galoping được
Bảng C.2 : Giá trị µ’DL (0)
C.4. Kết luận
- Đối với các công trình cao và kết cấu mềm cần phải kiểm tra tình trạng mất ổn định khí động
- Mất ổn định do kích động xoáy thường xảy ra với các kết cấu và công trình có tiết diện tròn với vận tốc gió trong một khoảng giới hạn nhất định. Lực khí động trong trường hợp này tác dụng chủ yếu lên một phạm vi của chiều cao công trình, phạm vi này càng cao thì lực khí động càng lớn.
- Mất ổn định galoping thường xảy ra với công trình cao và kết cấu mềm dạng lăng trụ, các công trình có tiết diện ngang dạng tròn nhưng mặt ngoài đón gió xù xì, góc cạnh, khi vận tốc gió lớn hơn vận tốc gió giới hạn.
- Có thể thiết kế để công trình chịu được lực khí động khi mất ổn định do kích động xoáy. Còn đối với mất ổn định dạng galoping thì phải thay đổi giải pháp thiết kế để công trình không rơi vào trạng thái mất ổn định này.
C.5. Ví dụ 1
Tìm chuyển vị ngang ở đỉnh và lực khí động cho công trình tháp bằng thép dạng hình trụ tròn, cao 90m có sơ đồ tính toán như hình C.5. Đường kính của công trình D = 5,3m ; số Strouhat Sh =0,22 ; tần số dao động f1 = 0,75 (Hz) ; hệ số lực µL = const = 0,2 ; tỉ lệ cản g = 0,02; hệ số m1 = 0,14; vận tốc gió ở độ cao 10m: v10 = 15m/s.
Vận tốc gió tới hạn:
![]()
Phạm vi tác động của kích động xoáy là :
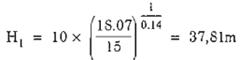
Ta có H1 = 37,81 mét < H = 90 mét, vậy có xảy ra hiện tượng cộng hưởng do kích động xoáy đối với công trình.
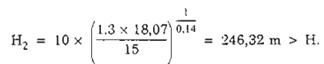
Lấy H2 = H = 90m
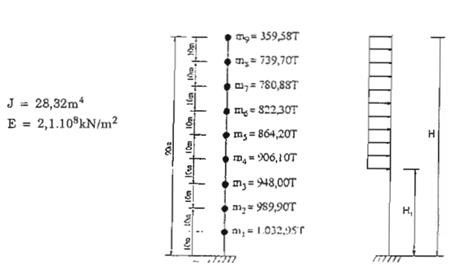
Hình C.5 : Sơ đồ tính toán động lực
Chuyển vị lớn nhất và tải trọng lớn nhất tác dụng lên công trình được xác định theo công thức :
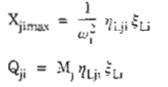
Trong đó :
![]()
wi – là tần số dao động riêng của công trình ứng với dạng dao động thứ i. Để đơn giản, ở đây chỉ xét dạng dao động thứ nhất có w1 = 2 Õ f1 = 4.71 Rad/s.
hLji – hệ số được xác định theo công thức :
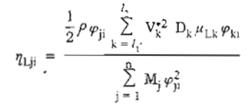
Với :
- V*k = V10 k (k là hệ số kể đến sự thay đổi áp lực gió theo độ cao và dạng địa hình ứng với các điểm tập trung khối lượng từ H1 đến H – Tra bảng 7) ;
- Dk – bề rộng mặt đón gió của công trình, lấy Dk = D = 5,3m ;
- µLk = const = 0,2 ;
- jki – dịch chuyển ngang tỉ đối theo phương ngang luồng gió của công trình tại điểm k ứng với dạng dao động thứ i ;
- Do H1 = 37,81m ; H2 = 90m nên lấy l1 tại điểm 4 có độ cao z4 = 40m và lấy l2 tại điểm 9 có độ cao z9 = 90m ;
- Mj – khối lượng tập trung của công trình đặt tại điểm thứ j ;
Kết quả tính chuyển vị và tải trọng lớn nhất tác dụng lên công trình tại điểm thứ j ứng với dạng dao động đầu tiên được cho trong bảng C.3.
Bảng C.3 : Giá trị Xljmax và Qlj của công trình
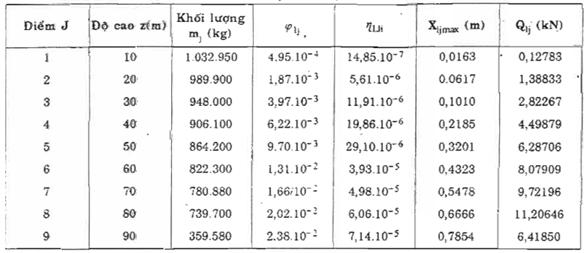
Vậy chuyển vị lớn nhất ở đỉnh công trình 0,7854m
C.6. Ví dụ 2
Kiểm tra mất ổn định khí động của một dầm thép thành mỏng hình vuông kích thước mặt cắt như hình C.6. Nhịp L = 12m, tốc độ gió thiết kế v = 44,5m/s ; tỉ cản của kết cấu g = 0,01.
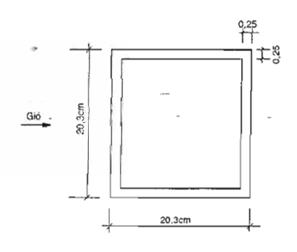
Hình C.6 : Mặt cắt dầm thép.
Môđun đàn hồi : E = 2.104 kN/cm2
Mômen quán tính chống uốn của tiết diện J = 1420 cm4
Diện tích tiết diện A = 20,5 cm2
Khối lượng phân bố : m = 1,678 x 106 kNs2cm2.
Mật độ không khí : p = 0,125 x 10-10 kN.s2cm4
Tần số dao động f1
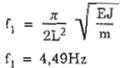
Từ bảng C.2 ta có :m'DL (0) = + 2,7
Hệ số cản:
C = 2gwm
C = 4pgf1m
C = 0,9468.106
Vận tốc gió tới hạn:
![]()
Vì v > v* nên dầm bị mất ổn định. Cần phải mở rộng kích thước của dầm.
PHỤ LỤC D
(Tham khảo)
VÍ DỤ TÍNH TOÁN
D.1. Ví dụ 1 :
Xác định thành phần động của tải trọng gió tác dụng lên nhà cao 21 tầng xây dựng ở Hà Nội. Chiều cao nhà H = + 77,7m ; kích thước mặt bằng D x L = 24m x 24m. Thời gian sử dụng 50 năm.
Mặt bằng bố trí kết cấu vách, lõi cứng và các khung của nhà xem hình D.1.
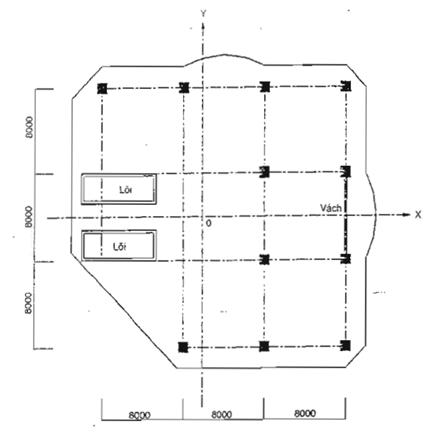
Hình D.1 : Sơ đồ mặt bằng công trình
Công trình có chiều cao H = 77,7m > 40m nên phải kể đến thành phần động của tải trọng gió.
D.1.1. Sơ đồ tính toán động lực
Độ cứng theo phương bất lợi của nhà EJv = 922529.515 kN.m2 ; 21 điểm tập trung khối lượng ứng với các mức sàn. Sơ đồ tính toán động lực của nhà lấy là một công xôn ngàm chặt vào đất, hình D.2.
D.1.2. Xác định các đặc trưng động lực
D.1.2.1. Xác định tần số dao động riêng

Hình D.2 : Sơ đồ tính toán động lực
Công trình có tiết diện và độ cứng không đổi theo chiều cao, tần số dao động riêng được xác định theo công thức B.24, phụ lục B
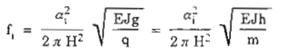
Trong đó :
a1 – hệ số ứng với dạng dao động riêng của công trình, với 3 dạng đầu tiên, ta có :
a1 = 1,875; a2 = 4,694; a3 = 7,86
H – chiều cao của công trình, H = 77,7m :
m – khối lượng của công trình trên một đơn vị dài theo chiều cao công trình (T/m) :
Do đó:

Vì f2 < fL < f3 (với vật liệu là giá trị giới hạn của tần số dao động riêng, theo bảng 2 có fL = 1,3), nên việc xác định thành phần động của tải trọng gió chỉ cần kể đến ảnh hưởng của hai dạng dao động đầu tiên.
D.1.2.2. Xác định các dạng dao động riêng
Biên độ dạng dao động riêng thứ i tại điểm j được xác định theo công thức
![]()
Với 3 dạng đầu tiên, ta có
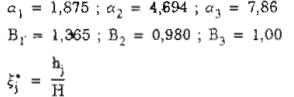
Với hj là khoảng cách từ điểm đặt khối lượng thứ j đến mặt móng của công trình.
Kết quả tính toán các giá trị yji của hai dạng dao động đầu tiên cho trong bảng D.1.
Bảng D.1. Biên độ của hai dạng dao động đầu tiên
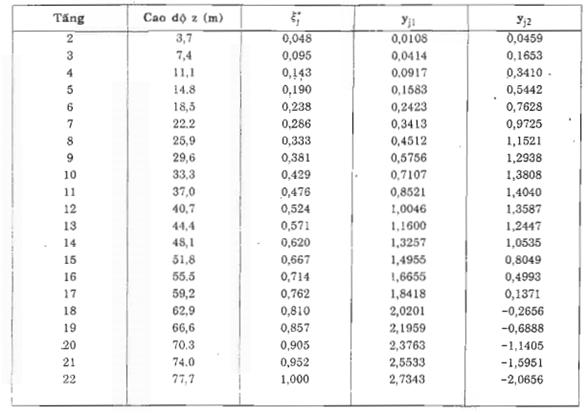
D.1.3. Xác định giá trị tiêu chuẩn thành phần tĩnh của áp lực gió tác dụng lên các phần tính toán của công trình.
Giá trị tiêu chuẩn thành phần tĩnh của áp lực gió Wj ở độ cao zj so với mốc chuẩn được xác định theo công thức (4.11).
![]()
Trong đó :
Wo – giá trị áp lực gió tiêu chuẩn. Công trình xây dựng ở Hà Nội thuộc vùng II – B,
Wo = 95daN/m2 = 0,95 kN/m2 ;
k(zj) – hệ số tính đến sự thay đổi áp lực gió theo độ cao, lấy theo bảng 7 ;
c – hệ số khí động. Phía đón gió cđ = 0,8 ; phía hút gió ch = 0,6
c = 0,8 + 0,6 = 1,4
Kết quả tính toán các giá trị Wj ứng với các phần tính toán của công trình
|
Tầng |
cao độ z(m) |
k |
Wj (kN/m2) |
|
1 |
2 |
3 |
4 |
|
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
3,7 7,4 11,1 14,8 18,5 22,2 25,9 29,6 33,3 37,0 40,7 44,4 48,1 51,8 55,5 59,2 62,9 66,6 70,3 74,0 77,7 |
0,828 0,938 1,018 1,077 1,115 1,150 1,183 1,216 1,240 1,262 1,284 1,306 1,329 1,347 1,362 1,377 1,390 1,403 1,416 1,429 1,442 |
1,10124 1,24754 1,35394 1,43241 1,48295 1,52950 1,57339 1,61728 1,64920 1,67846 1,70772 1,73698 1,76757 1,79151 1,81146 1,83141 1,84870 1,86599 1,88328 1,90057 1,91786 |
D.1.4. Xác định thành phần động của tải trọng gió tác dụng lên công trình.
Giá trị tiêu chuẩn thành phần động của tải trọng gió tác dụng lên phần thứ j (có độ cao z) ứng với dạng dao động riêng thứ j được xác định theo công thức (4.3).
![]()
Trong đó :
Mj – khối lượng tập trung của phần công trình thứ j ;
xi - hệ số động lực ứng với dạng dao động thứ j :
ym – dịch chuyển ngang tỉ đối của trọng tâm phần công trình thứ j ứng với dạng dao động thứ i ;
yi – hệ số được xác định bằng cách chia công trình thành n phần, trong phạm vi mỗi phần tải trọng gió có thể coi như không đổi
a) Xác định hệ số yi
Hệ số yi được xác định bằng công thức (4.5).
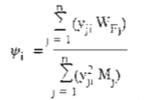
Với VFj : giá trị tiêu chuẩn thành phần động của tải trọng gió tác dụng lên phần thứ j của công trình, ứng các dạng dao động khác nhau khi chỉ kể đến ảnh hưởng của xung vận tốc gió, được xác định theo công thức :
![]()
Trong đó : Wj – đã xác định trong bảng D.2 ;
Dj, hj - bề rộng và chiều cao của mặt đón gió ứng với phần thứ j ;
xi - hệ số áp lực động của tải trọng gió ở độ cao z ứng với phần thứ j của công trình, tra bảng 3 ,
v – hệ số tương quan không gian áp lực động của tải trọng gió được xác định phụ thuộc vào tham số p, x và dạng dao động. Với mặt phẳng tọa độ cơ bản song song với bề mặt tính toán zOx, ta có :
p = D = 24m ; x = H = 77,7m.
Từ bảng 4 và bảng 5, ta có : đối với dạng dao động thứ nhất, v1 = 0,673 ; còn đối với dạng dao động thứ hai, v2 lấy bằng 1.
Kết quả tính toán WFj cho trong bảng D.3.
Bảng D.3 : Các giá trị WFj
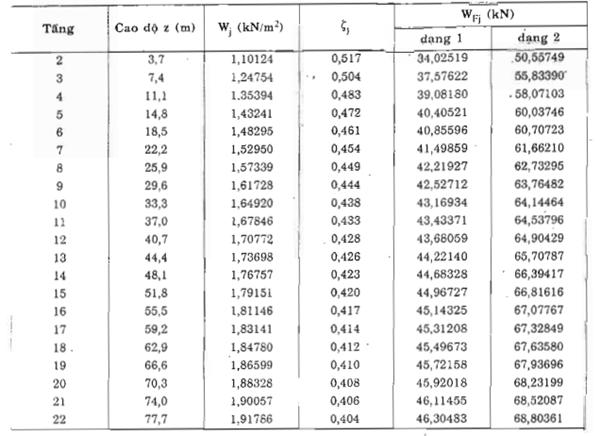
Từ các giá trị của Mj, yji và WFj, ta xác định được hệ số yi ứng với 2 dạng dao động đầu tiên :
y1 = 0,0229 : y2 = 0,017
b) Xác định hệ số động lực xi
Hệ số động lực xi , xác định phụ thuộc vào thông số ei và độ giảm loga của dao động d.
Thông số ei xác định theo công thức (4.4).
![]()
Trong đó :
g – là hệ số tin cậy của tải trọng gió lấy bằng 1,2 ;
fi – tần số dao động riêng thứ i ;
Wo – lấy bằng 950 N/m2.
Ở đây công trình bằng bêtông cốt thép nên có d = 0,3. Theo đồ thị hình 1, xác định được hệ số động lực xi như trong bảng D.4.
Bảng D.4 : Hệ số động lực xi ứng với 2 dạng dao động riêng đầu tiên.

c) Xác định thành phần động của tải trọng gió
Từ giá trị Mj, xi, yi và yji, ta xác định được các giá trị tiêu chuẩn thành phần động của tải trọng gió Wp(ji).
Giá trị tính toán thành phần động của tải trọng gió được xác định theo công thức (4.10):
![]()
Trong đó:
g - hệ số độ tin cậy đối với tải trọng gió; lấy bằng 1,2;
b - hệ số điều chỉnh tải trọng gió theo thời gian; lấy bằng 1,0.
Kết quả các giá trị tiêu chuẩn và các giá trị tính toán thành phần động của tải trọng gió cho trong bảng D.5.
Bảng D.5 : Các giá
trị Wp(ji) và ![]()
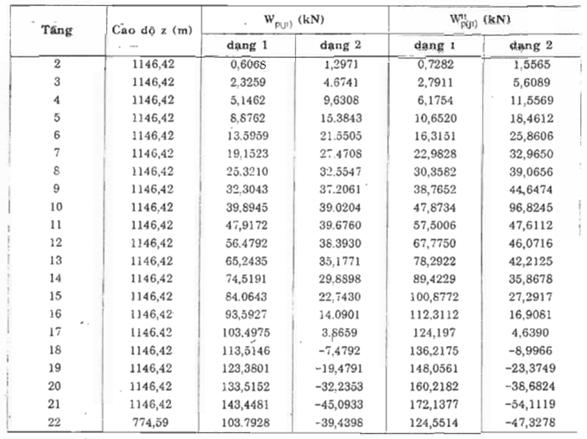
D.2. Ví dụ 2: Xác định thành phần động của tải trọng gió lên cột điện bằng thép.
Cột được xây dựng ở vùng II, địa hình dạng B, giá trị áp lực gió tiêu chuẩn bằng 95daN/m2. Cột có kết cấu không gian bằng các thép ống có các đường kính khác nhau. Các tiết diện của cột là hình vuông, kích thước hình học của cột cho trong hình D.3a.
Chọn mô hình tính toán cột có dạng là thanh công xôn ngàm vào đất với các khối lượng tập trung như trong hình D.3b.
D.2.1. Xác định tần số và dạng dao động riêng cơ bản của công trình
Tần số dao động riêng cơ bản của công trình được tính bằng công thức (B.28), phụ lục B.
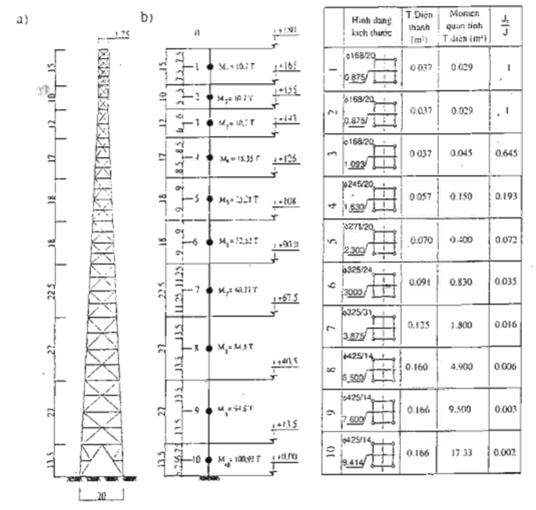
Hình D.3 : Kích thước hình học và sơ đồ tính toán của cột điện
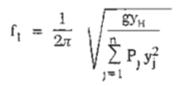
Trong đó:
Pj – là trọng lượng của đoạn công trình thứ j, tính bằng kN;
yH, yj – là chuyển vị tại đỉnh và trọng tâm đoạn thứ j của công trình, đo lực bằng đơn vị (1kN) đặt tại đỉnh công trình gây ra.
Kết quả tính toán yH, yj,
và Pj, ![]() được cho trong bảng D.6.
được cho trong bảng D.6.
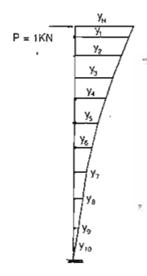
Hình D.4 : Các chuyển vị yH và yj do lực P = 1 kn đặt tại đỉnh gây ra.
Bảng D.6 : Các giá
trị yj và Pj, ![]()
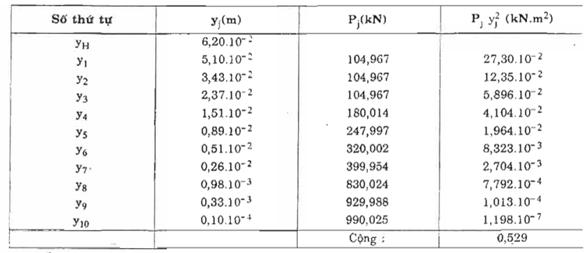
Vậy tần số dao động riêng thứ nhất của công trình sẽ là:
![]()
Do đó thành phần động của tải trọng gió phải kể đến ảnh hưởng của cả phần xung vận tốc gió và phần quán tính của công trình. Trong ví dụ này, để đơn giản, ta chỉ tính ảnh hưởng của dạng dao động riêng thứ nhất đến giá trị thành phần động của tải trọng gió.
Dạng dao động riêng cơ bản trong trường hợp này có thể lấy gần đúng theo đường đàn hồi của hệ, do lực P = 1kN đặt ở đỉnh gây ra [6] đã cho trong bảng D.6.
D.2.2. Xác định giá trị tiêu chuẩn thành phần tĩnh của áp lực gió tác dụng lên các phần tính toán của công trình.
Giá trị tiêu chuẩn thành phần tĩnh của áp lực gió được xác định theo công thức (4.11)
Wj = Wok(zj)c
Trong đó:
Wo – lấy bằng 95 daN/m2 = 0,95kN/m2;
k(zj) – hệ số tính đến sự thay đổi áp lực gió theo độ cao;
c – hệ số cản chính diện đối với công trình có dạng giàn không gian và tháp rỗng, được tính theo công thức:
c = cx (1 + h) kj
a) Xác định hệ số cản chính diện c
cx – hệ số khí động đối với một giàn phẳng độc lập
![]()
Trong đó:
cxi – hệ số khí động của cấu kiện thứ i xác định trong bảng 6 trong TCVN 2737 : 1995;
Ai – diện tích hình chiếu của cấu kiện thứ i lên mặt phẳng đón gió của giàn;
A – diện tích giới hạn đường bao ngoài của giàn.
Cụ thể, xét đoạn cột 7, hệ số khí động đối với từng cấu kiện cho trong bảng D.7.
Bảng D.7 : Hệ số khí động cxi đối với từng loại thanh của đoạn cột 7

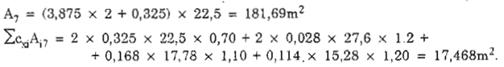
Vậy hệ số cx bằng
![]()
h - hệ số phụ thuộc vào hệ số choán j của kết cấu và Rc.
Hệ số choán j được xác định bằng công thức:

Do đó:
![]()
Đối với đoạn 7, tra bảng ta có h7 = 0,95
k1 – hệ số phụ thuộc vào hướng gió, tra bảng có k1 = 1,2 x 0,9 (ở đây 0,9 là hệ số đối với tháp tổ hợp từ thép đơn).
Vậy, hệ số cản chính diện sẽ bằng:
c7 = 0,094 x (1 + 0,95) x 1,2 x 0,9 = 0,206
b) Xác định hệ số tính đến sự thay đổi áp lực gió theo độ cao k (zj).
Đối với đoạn 7, tại cao trình z7 = +78,75m, với địa hình dạng B, ta có k7 = 1,446.
Vậy, giá trị tiêu chuẩn thành phần tĩnh của áp lực gió tại đoạn 7 sẽ là:
W7 = 0,95 x 1,446 x 0,206 = 0,28298 kN/m2
D.2.3. Xác định thành phần động của tải trọng gió tác dụng lên công trình.
Giá trị tiêu chuẩn thành phần động của tải trọng gió được xác định theo công thức (4.3). Khi chỉ xét với dạng dao động cơ bản, công thức này có dạng:
![]()
Trong đó:
Mj - khối lượng của phần công trình thứ j có trọng tâm ở độ cao z.
x - hệ số động lực ứng với dạng dao động cơ bản:
yj - dịch chuyển ngang tỉ đối của phần công trình thứ j ở độ cao z ứng với dạng dao động cơ bản;
y - hệ số được xác định bằng cách chia công trình thành n phần trong phạm vi mỗi phần tải trọng gió có thể coi như không đổi.
a) Xác định hệ số y:
Hệ số y được xác định theo công thức (4.5). Khi chỉ xét với dạng dao động cơ bản, công thức này có dạng:
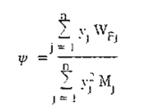
Trong đó:
yj - gần đúng lấy bằng các giá trị trong cột 2 của bảng D.6;
WFj - giá trị tiêu chuẩn thành phần động của tải trọng gió tác dụng lên phần thứ j của công trình ứng với dạng dao động thứ nhất, khi chỉ kể đến ảnh hưởng của xung vận tốc gió, được xác định theo công thức (4.6).
![]()
Trong đó:
Wj - đã xác định ở phần D.2.2; W7 = 0.28298 kN/m2;
zj - hệ số áp lực của tải trọng gió ở phần thứ j của công trình;
v - hệ số tương quan không gian, ở đây v lấy bằng vj tương ứng với dạng dao động cơ bản.
Xét đoạn cột 7, tại đây có khối lượng M7 = 40,77t. đặt tại cao trình 78.75m. Công trình được xây dựng ở địa hình dạng B, tra bảng có x7 = 0.404.
Hệ số tương quan không gian vj xác định phụ thuộc vào các tham số p, g và dạng dao động.
Ta có: p = D, với D lấy bằng bề rộng đón gió của cột điện tại tiết diện ở 2/3 chiều cao cột:
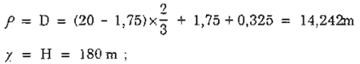
Từ bảng 4 và 5, ta có vj = 0,616
S7 - Diện tích đón gió lấy bằng diện tích giới hạn bởi đường bao ngoài của phần cột, S7 = A7.
Vậy:
WF7 = 0,28298 x 0,404 x 0,616 x 181,69 = 12,79525 kN
Tương tự như trên, ta tính được giá trị WFj ở các phần khác của công trình. Các kết quả cho trong bảng D.8.
Bảng D.8 : Các giá trị WFj, yj, Mj
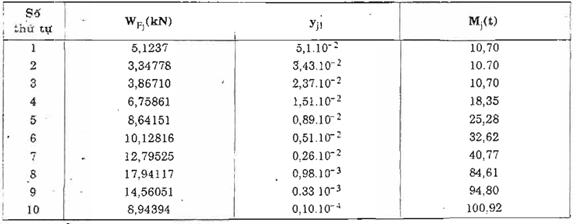
b) Xác định hệ số động lực x
Hệ số động lực x được xác định theo đồ thị hình 1 phụ thuộc vào thông số e và độ giảm loga của dao động d
Thông số e được xác định theo công thức (4.4):
![]()
Trong đó:
g - là hệ số tin cậy của tải trọng gió, lấy g = 1,2;
Wo - giá trị tiêu chuẩn của áp lực gió, lấy Wo = 950N/m2;
f - tần số của dạng dao động riêng cơ bản.
Vậy:

Vì công trình có dạng trụ thép nên có độ giảm loga của dao động d = 0,15
Tra bảng, có hệ số động lực x = 2,8.
c) Xác định Wpj và ![]()
Từ các giá trị Mj, x, y và yji tìm được ở trên, ta xác định được các giá trị tiêu chuẩn thành phần động của tải trọng gió Wpj tác dụng lên các phần của công trình.
Giá trị tính toán thành phần động của tải trọng gió được xác định bằng công thức (4.10):
![]()
Trong đó:
g - hệ số tin cậy đối với tải trọng gió, g = 1,2;
b - hệ số điều chỉnh tải trọng gió theo thời gian sử dụng giả định của công trình. Với công trình có thời gian sử dụng 50 năm, lấy b = 1.
Kết quả tính toán các giá trị Wpj
và ![]() cho trong bảng D.9.
cho trong bảng D.9.
Bảng D.9 : Các giá
trị Wpj và ![]()
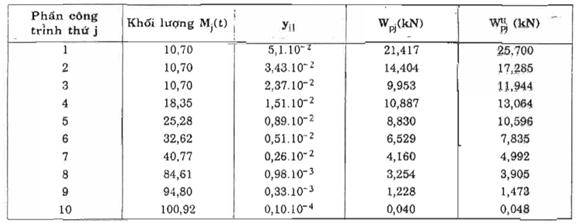
D.3. Ví dụ 3: Xác định thành phần động của tải trọng gió lên ống khói bê tông cốt thép, xây dựng trong vùng IIB. Ống khói cao H = 180m, bằng bê tông mác M250 (Eb = 2.8.107 kN/m2), mô men quán tính tiết diện đáy ống khói Jo = 1020m4; diện tích tiết diện đáy ống khói Fo = 40,1m2; mômen quán tính của tiết diện ở đỉnh ống khói : jH = 22,1m4; diện tích đế móng: Fm = 615m2. Lớp lót của thân ống khói tựa lên các bậc công xôn bằng bê tông cốt thép và xây bằng gạch chịu lửa. Giữa thành bê tông và lớp lót có lớp bông khoáng cách nhiệt.
Trọng lượng thể tích của vật liệu làm thân ống khói và lớp lót là:
qth = 24kN/m3; qj = 14kN/m3
Diện tích tiết diện ngang của phần thân và phần lớp lót ứng với cao độ trung bình của ống khói là:
Fth = 5,2m2; Fl = 6.56m2
Phần đỉnh của ống khói cao 10m dùng gạch chịu axít và đặt cốt thép dọc. Móng ống khói là móng bè, đường kính 28m. Hệ số nén Cz = 60000 kN/m2. Sơ đồ hình học ống khói cho trong hình D.5a.
Chia ống khói thành 15 phần, khối lượng của mỗi một phần đặt tập trung ở giữa mỗi đoạn. Sơ đồ tính toán động lực cho trong hình D.5b.
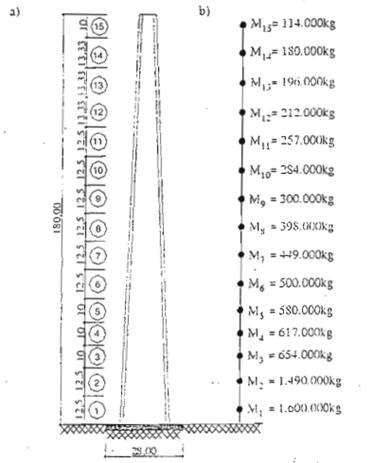
Hình D.5 : Sơ đồ hình học và sơ đồ tính toán ống khói
D.3.1. Xác định tần số và dạng dao động riêng của công trình
D.3.1.1. Xác định tần số dao động riêng
Tần số dao động riêng thứ i (fi) của công trình dạng ống khói, có kể đến ảnh hưởng của biến dạng nén, được xác định theo công thức (B.29), phụ lục B.
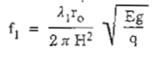
Trong đó:
H - chiều cao ống khói tính đến mặt của móng, H = 180m;
E - là môđun đàn hồi của vật liệu làm ống khói, E = 2,8.107 kN/m2;
ro - bán kính quán tính của tiết diện đáy ống khói (m), được xác định bằng công thức:
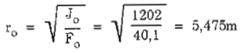
q - trọng lượng thể tích của thân ống khói, q được tính bằng công thức (B.31)
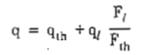
Vậy:
![]()
li - hệ số ứng với dạng dao động thứ i, phụ thuộc vào các tham số:
![]()
Theo biểu đồ hình B.2, phụ lục B, ta có hệ số l ứng với 3 dạng đầu tiên là
l1 = 4,9 l2 = 18,7 l3 = 35
Vậy, tần số dao động riêng của ống khói theo 3 dạng đầu tiên sẽ là
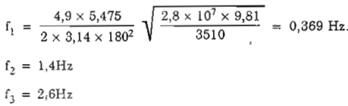
Vì f3 < fL (Với fL là giá trị giới hạn của tần số dao động riêng của ống khói có độ giảm loga dao động = 0,15; theo bảng 2 có fL = 4,1), trong ví dụ này, để đơn giản, ta chỉ kể đến ảnh hưởng 3 dạng dao động đầu tiên.
D.3.1.2. Xác định các dạng dao động riêng
Biên độ dao động riêng thứ i tại điểm j của ống khói được xác định theo công thức (B.32)
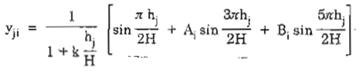
Trong đó:
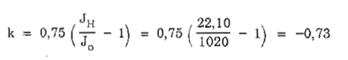
hj - là chiều cao từ đáy ống khói đến điểm đang xét (m)
Ai, Bi - là hệ số ứng với các dạng dao động;
Với:
![]()
theo các biểu đồ hình B.3, phụ lục B, ta có:
A1 = 0,195 A2 = 5,8 A3 = 9,5
B1 = 0,011 B2 = -1,5 B3 = 27
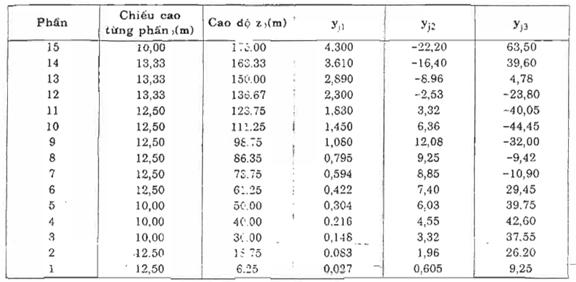
Kết quả tính toán các giá trị yji của 3 dạng dao động đầu tiên cho trong bảng D.9.
Bảng D.10 : Dịch chuyển ngang tỉ đối của 3 dạng dao động đầu tiên
D.3.2. Xác định giá trị tiêu chuẩn thành phần tĩnh của áp lực gió tác dụng lên các phần tính toán của công trình.
Giá trị tiêu chuẩn thành phần tĩnh của áp lực gió Wj ở độ cao z so với mốc chuẩn được xác định theo công thức (4.11)
![]()
Trong đó:
Wo - là giá trị áp lực gió tiêu chuẩn, Wo = 95daN/m2 = 0,95kN/m2;
k(zj) - là hệ số tính đến sự thay đổi áp lực gió theo độ cao, lấy theo bảng 7;
c - hệ số khí động. Đối với công trình hình trụ tròn ta lấy giá trị trung bình. Theo bảng 6 TCVN 2737 : 1995, lấy c = 0,8.
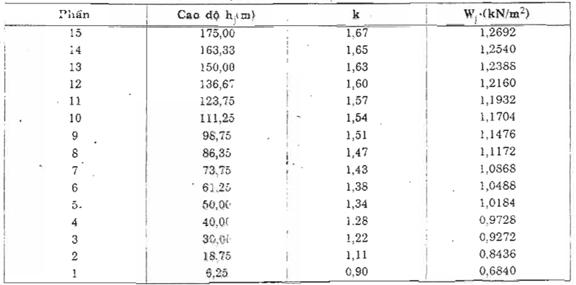
Kết quả tính toán các giá trị Wj cho trong bảng D.10.
Bảng D.11 : Các giá trị Wj ứng với các phần tính toán của công trình
D.3.3. Xác định thành phần động của tải trọng gió
Giá trị tiêu chuẩn thành phần động của tải trọng gió tác dụng lên phần thứ j (có cao độ z) ứng với dạng dao động riêng thứ i được xác định theo công thức (4.3)
![]()
Trong đó:
Mj - khối lượng tập trung của phần công trình thứ j;
xi - hệ số động lực ứng với dạng dao động thứ i;
yji - dịch chuyển ngang tỉ đối của trọng tâm phần công trình thứ j ứng với dạng dao động thứ i;
yi - hệ số được xác định bằng cách chia công trình thành n phần, trong phạm vi mỗi phần tải trọng gió có thể coi như không đổi.
a) Xác định hệ số yi
Hệ số yi được xác định bằng công thức (4.5)
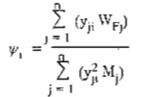
Với WFj - giá trị tiêu chuẩn thành phần động của tải trọng gió tác dụng lên phần thứ j của công trình, ứng với các dạng dao động khác nhau khi chỉ kể đến ảnh hưởng của xung vận tốc gió, được xác định theo công thức:
![]()
Trong đó:
Wj - đã xác định trong bảng D.10:
Dj, hj - bề rộng và chiều cao của mặt đón gió ứng với phần thứ j;
zj - hệ số áp lực động của tải trọng gió ở độ cao z ứng với phần thứ j của công trình, tra bảng 3;
v - hệ số tương quan không gian áp lực động của tải trọng gió được xác định phụ thuộc vào tham số p, g và dạng dao động, ta có: p = D; (D là đường kính trung bình của ống khói bằng 9m)
p = 9m; g = H = 180m.
Từ bảng 4 và 5, ta có: đối với dạng dao động thứ nhất, v1 = 0,63; Còn đối với dạng dao động thứ hai và thứ ba, v2 và v3 lấy = 1.
Kết quả tính toán WFj cho trong bảng D.11.
Bảng D.12: Các giá trị WFj
|
Phần |
Cao độ z(m) |
hj (m) |
dj (m) |
zj |
Wj (kN/m2) |
WFj (kN) |
|
|
dạng 1 |
dạng 2 và 3 |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 |
175,00 163,33 150,00 136,67 123,75 111,25 98,75 86,35 73,75 61,25 50,00 40,00 30,00 18,75 6,25 |
10,00 13,33 13,33 13,33 12,50 12,50 12,50 12,50 12,50 12,50 10,00 10,00 10,00 12,50 12,50 |
5,80 6,10 6,50 6,90 7,30 7,80 8,30 8,80 9,57 10,30 11,00 11,70 12,40 13,10 14,10 |
0,376 0,378 0,381 0,385 0,388 0,392 0,396 0,400 0,407 0,418 0,422 0,429 0,443 0,460 0,514 |
1,2692 1,2540 1,2388 1,2160 1,1932 1,1704 1,1476 1,1172 1,0868 1,0488 1,0184 0,9728 0,9272 0,8436 0,6840 |
17,4356 24,2823 25,7638 27,1278 26,6145 28,1816 29,7040 30,9688 33,3355 35,1342 29,7827 30,7615 32,0878 40,0328 39,0381 |
27,6787 35,5433 40,8950 43,0600 42,2453 44,7327 47,1492 49,1568 52,9134 55,7686 47,2741 48,8278 50,9330 63,5442 61,9653 |
Từ các giá trị của Mj, yji và WFj, ta xác định được hệ số i, ứng với 3 dạng dao động đầu tiên
y1 = 0,0052; y2 = 0,00045; y3 = 0,00011
b) Xác định hệ số động lực xj
Hệ số động lực xj xác định phụ thuộc vào thông số ei và độ giảm loga của dao động d
Thông số ei xác định theo công thức (4.4).
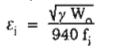
Trong đó:
g - là hệ số tin cậy của tải trọng gió lấy bằng 1,2;
fi - tần số dao động riêng thứ i;
Wo - lấy bằng 950N/m2.
Ở đây, công trình có d = 0,15. Theo đồ thị hình 1, ta xác định được hệ số động lực xj
x1 = 2,4 2 x2= 1,75 x3 = 1,56
c) Xác định thành phần động của tải trọng gió.
Từ các giá trị Mj, xj, yji và yji ta xác định được giá trị tiêu chuẩn thành phần động Wp(ji).
Giá trị tính toán thành phần động của tải trọng gió được xác định theo công thức (4.10);
![]()
Trong đó:
g - hệ số độ tin cậy đối với tải trọng gió; g lấy bằng 1,2;
b - hệ số điều chỉnh tải trọng gió theo thời gian ; b lấy bằng 1,0.
Kết quả các giá trị tiêu chuẩn và các giá trị tính toán thành phần động của tải trọng gió cho trong bảng D.12.
Bảng D.13 : Các giá
trị Wp(ji) và ![]()
|
Phần |
Cao độ z(m) |
Wp(ji) (kN) |
|
||||
|
dạng 1 |
dạng 2 |
dạng 3 |
dạng 1 |
dạng 2 |
dạng 3 |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 |
175,00 163,33 150,00 136,67 123,75 111,25 98,75 86,35 73,75 61,25 50,00 40,00 30,00 18,75 6,25 |
61,1770 81,0951 70,6917 60,8515 58,6947 51,3926 40,4352 39,4880 33,2849 26,3328 22,0047 16,6324 12,0796 15,4340 5,3914 |
-19,9301 -23,2470 -13,8298 -4,2238 6,7193 14,2241 28,5390 28,9918 31,2925 29,1375 27,5420 22,1079 17,0988 22,9982 7,6230 |
12,4221 12,2317 1,6077 -8,6583 -17,6625 -21,6624 -16,4736 -6,4336 8,3983 25,2681 39,5624 45,1037 42,1410 66,9892 25,3968 |
73,4124 97,3141 84,8300 73,0230 70,4336 61,6712 48,5222 47,3856 39,9419 31,5994 26,4057 19,9588 14,4956 18,5208 6,4696 |
-23,9161 -27,8964 -16,5957 -5,0686 8,0631 17,0690 34,2468 34,7902 37,5510 34,9650 33,0504 26,5295 20,5186 27,5978 9,1476 |
14,9066 14,6780 1,9292 -10,3899 -21,1950 -25,9949 -16,7683 -7,7203 10,0779 30,3217 47,4749 51,1244 50,5692 80,3871 30,4762 |
TÀI LIỆU THAM KHẢO
1. Tải trọng và tác động – Tiêu chuẩn thiết kế. TCVN 2737 : 1995. Nhà xuất bản Xây dựng Hà Nội.
2. Trương Tương Đình – Tính toán tải trọng gió và sổ tay tính toán chống gió. Nhà xuất bản Đại học Đồng tế Thượng Hải 1990, (bản Trung văn).
3. Báo cáo tổng kết đề tài 26B.03.01. “Nghiên cứu phương pháp tính toán công trình có kể đến tải trọng động đất và gió bão”. Viện KHKT Xây dựng – 1998.
4. Báo cáo tổng kết đề tài 02.15.14 – RO1. “Một số biện pháp phòng chống bão trong xây dựng”. Viện KHKT Xây dựng – 1992.
5. … 1984, 358 c.
6. … 1978, 216 c.
7. G.A Dobrodzicki, Flow Visualization in the National Aerounautical Establishment’s Water tunnel. Aeronautical Report No.LR – 557. National Research Council of Canada. Ottawa, 1972.
8. G.e. Mattingly, An experimental Study of the Thre- Dimensionnality of the Flow Around a Circular Cylinder, Report No. BN295, Institute for Fluid Dynamics and Applied Mathematics, University of Maryland, College Park, … June 1972.
9. C. Farell, O.Guven and F.Maisch, “Mean Wind loading on Rough- Walled Cooling Towers”, J.Eng. Mech. Div., ASCE, 102, No.EM 6. Proc. paper 12647 (1976) 1059 – 1081
10. Ray W.Clough, Joseph Penzien. Dynamics of Structures.
11. C.S Durst, “Wind speeds over short periods of time. Meteor, May., 89 (1960) 181 – 186.
MỤC LỤC
Lời nói đầu
1. Phạm vi áp dụng
2. Nguyên tắc cơ bản
3. Trình tự các bước tính toán xác định thành phần động của tải trọng gió
4. Xác định thành phần động của tải trọng gió theo TCVN 2737 : 1995
Phụ lục A. Thiết lập các công thức tính toán thành phần động của tải trọng gió
A.1. Phản ứng của công trình và thành phần động của tải trọng gió
A.2. Hệ số độ cao k
A.3. Hệ số áp lực động của tải trọng gió z
A.4. Hệ số tương quan không gian g
A.5. Hệ số động lực x
Phụ lục B. Xác định các đặc trưng động lực
B.1. Xác định tần số và dạng dao động của hệ kết cấu dạng thanh công xôn có hữu hạn khối lượng tập trung
B.2. Công trình có sơ đồ tính toán là thanh công xôn có khối lượng phân bố đều
B.3. Một số công thức thực nghiệm
Phụ lục C. Kiểm tra mất ổn định khí động cho công trình cao và kết cấu mềm
C.1. Đặt vấn đề
C.2. Mất ổn định do kích động xoáy đối với kết cấu và công trình dạng trụ tròn
C.3. Mất ổn định khí động dạng galoping đối với kết cấu và công trình dạng lăng trụ
C.4. Kết luận
C.5. Ví dụ 1
C.6. Ví dụ 2
Phụ lục D. Ví dụ tính toán
D.1. Ví dụ 141
D.2. Ví dụ 2
D.3. Ví dụ 3
Tài liệu tham khảo
